Намерете дължината на голямата ос на елипсоида. Линии от втори ред. Елипса и нейното канонично уравнение. кръг

11.1. Основни понятия

Разгледайте линиите, определени от уравнения от втора степен по отношение на текущите координати

Коефициентите на уравнението са реални числа, но поне едно от числата A, B или C е различно от нула. Такива линии се наричат ​​линии (криви) от втори ред. По-долу ще бъде установено, че уравнение (11.1) определя окръжност, елипса, хипербола или парабола в равнината. Преди да пристъпим към това твърдение, нека проучим свойствата на изброените криви.

11.2. кръг

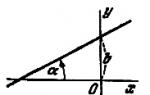
Най-простата крива от втори ред е кръг. Припомнете си, че окръжност с радиус R с център в точка е множеството от всички точки Μ на равнината, които отговарят на условието . Нека точка в правоъгълна координатна система има координати x 0, y 0 a - произволна точка от окръжността (виж фиг. 48).

Тогава от условието получаваме уравнението

(11.2)

Уравнение (11.2) е изпълнено от координатите на която и да е точка от дадения кръг и не е изпълнено от координатите на която и да е точка, която не лежи на кръга.

Уравнение (11.2) се нарича каноничното уравнение на окръжността

По-специално, приемайки и , получаваме уравнението на окръжност с център в началото .

Уравнението на кръга (11.2) след прости трансформации ще приеме формата . При сравняване на това уравнение с общото уравнение (11.1) на крива от втори ред е лесно да се види, че са изпълнени две условия за уравнението на окръжност:

1) коефициентите при x 2 и y 2 са равни един на друг;

2) няма член, съдържащ xy произведението на текущите координати.

Нека разгледаме обратната задача. Поставяйки в уравнение (11.1) стойностите и , получаваме

Нека трансформираме това уравнение:

(11.4)

От това следва, че уравнение (11.3) определя окръжност при условието . Центърът му е в точката , и радиуса

.

Ако , то уравнението (11.3) има формата

.

Тя се удовлетворява от координатите на една точка . В този случай те казват: „окръжността се е изродила в точка“ (има нулев радиус).

Ако , тогава уравнение (11.4) и следователно еквивалентното уравнение (11.3) няма да определят права, тъй като дясната страна на уравнение (11.4) е отрицателна, а лявата страна не е отрицателна (да кажем: „въображаем кръг“).

11.3. Елипса

Канонично уравнение на елипса

Елипса е множеството от всички точки на равнината, сумата от разстоянията от всяка от тях до две дадени точки на тази равнина, т.нар. трикове , е постоянна стойност, по-голяма от разстоянието между фокусите.

Означете фокусите с F1и F2, разстоянието между тях в 2 ° С, а сумата от разстоянията от произволна точка на елипсата до фокусите - през 2 а(виж фиг. 49). По дефиниция 2 а > 2° С, т.е. а > ° С.

За да изведем уравнението на елипса, ние избираме координатна система, така че фокусите F1и F2лежат на оста , а началото съвпада със средата на отсечката F 1 F 2. Тогава фокусите ще имат следните координати: и .

Нека е произволна точка от елипсата. Тогава, според определението за елипса, т.е.

Това всъщност е уравнението на елипса.

Преобразуваме уравнение (11.5) в по-проста форма, както следва:

защото а>с, тогава . Да сложим

(11.6)

Тогава последното уравнение приема формата или

(11.7)

Може да се докаже, че уравнение (11.7) е еквивалентно на първоначалното уравнение. Нарича се каноничното уравнение на елипсата .

Елипса е крива от втори ред.

Изследване на формата на елипса според нейното уравнение

Нека установим формата на елипсата, използвайки нейното канонично уравнение.

1. Уравнение (11.7) съдържа x и y само в четни степени, така че ако точка принадлежи на елипса, тогава точките ,, също ѝ принадлежат. От това следва, че елипсата е симетрична по отношение на осите и , както и по отношение на точката , която се нарича център на елипсата.

2. Намерете точките на пресичане на елипсата с координатните оси. Поставяйки , намираме две точки и , в които оста пресича елипсата (виж фиг. 50). Поставяйки в уравнение (11.7), намираме точките на пресичане на елипсата с оста: и . точки А 1 , A2 , B1, B2Наречен върховете на елипсата. Сегменти А 1 A2и B1 B2, както и техните дължини 2 аи 2 bсе наричат ​​съответно големи и второстепенни осиелипса. Числа аи bсе наричат ​​съответно големи и малки. полуоскиелипса.

3. От уравнение (11.7) следва, че всеки член от лявата страна не превишава единица, т.е. има неравенства и или и . Следователно всички точки на елипсата лежат вътре в правоъгълника, образуван от правите линии.

4. В уравнение (11.7) сумата от неотрицателните членове и е равна на единица. Следователно, когато един член се увеличава, другият ще намалява, тоест, ако се увеличава, тогава намалява и обратно.

От казаното следва, че елипсата има формата, показана на фиг. 50 (овална затворена крива).

Повече за елипсата

Формата на елипсата зависи от съотношението. Когато елипсата се превърне в кръг, уравнението на елипсата (11.7) приема формата . Като характеристика на формата на елипса по-често се използва отношението. Съотношението на половината от разстоянието между фокусите към голямата полуос на елипсата се нарича ексцентричност на елипсата и o6o се обозначава с буквата ε („епсилон“):

с 0<ε< 1, так как 0<с<а. С учетом равенства (11.6) формулу (11.8) можно переписать в виде

Това показва, че колкото по-малък е ексцентрицитетът на елипсата, толкова по-малко сплескана ще бъде елипсата; ако поставим ε = 0, тогава елипсата се превръща в кръг.

Нека M(x; y) е произволна точка от елипсата с фокуси F 1 и F 2 (виж фиг. 51). Дължините на отсечките F 1 M=r 1 и F 2 M = r 2 се наричат ​​фокални радиуси на точката M. очевидно,

Има формули

Правите се наричат

Теорема 11.1.Ако е разстоянието от произволна точка на елипсата до някакъв фокус, d е разстоянието от същата точка до директрисата, съответстваща на този фокус, тогава отношението е постоянна стойност, равна на ексцентрицитета на елипсата:

От равенството (11.6) следва, че . Ако , тогава уравнение (11.7) дефинира елипса, чиято голяма ос лежи на оста Oy, а малката ос лежи на оста Ox (виж Фиг. 52). Фокусите на такава елипса са в точките и , където .

11.4. Хипербола

Канонично уравнение на хипербола

Хипербола се нарича множеството от всички точки на равнината, модулът на разликата в разстоянията от всяка от които до две дадени точки на тази равнина, т.нар. трикове , е постоянна стойност, по-малка от разстоянието между фокусите.

Означете фокусите с F1и F2разстоянието между тях през 2s, и модулът на разликата в разстоянията от всяка точка на хиперболата до фокусите през 2а. По дефиниция 2а < 2s, т.е. а < ° С.

За да изведем уравнението на хиперболата, ние избираме координатна система, така че фокусите F1и F2лежат на оста , а началото съвпадна със средата на сегмента F 1 F 2(виж фиг. 53). Тогава фокусите ще имат координати и

Нека е произволна точка от хиперболата. Тогава според определението за хипербола или , т.е. след опростяване, както беше направено при извеждането на уравнението на елипсата, получаваме канонично уравнение на хипербола

(11.9)

(11.10)

Хиперболата е линия от втори ред.

Изследване на формата на хипербола според нейното уравнение

Нека установим формата на хиперболата, използвайки нейното каконично уравнение.

1. Уравнение (11.9) съдържа x и y само в четни степени. Следователно хиперболата е симетрична по отношение на осите и , както и по отношение на точката , която се нарича центъра на хиперболата.

2. Намерете пресечните точки на хиперболата с координатните оси. Поставяйки в уравнение (11.9), намираме две точки на пресичане на хиперболата с оста: и . Поставяйки (11.9), получаваме , което не може да бъде. Следователно хиперболата не пресича оста y.

Точките и се наричат върхове хиперболи и отсечката

реална ос , отсечка - реална полуос хипербола.

Отсечката, свързваща точките, се нарича въображаема ос , номер b - въображаема ос . Правоъгълник със страни 2аи 2бНаречен основният правоъгълник на хипербола .

3. От уравнение (11.9) следва, че умаляваното не е по-малко от едно, т.е. или . Това означава, че точките на хиперболата са разположени отдясно на правата (дясното разклонение на хиперболата) и отляво на правата (лявото разклонение на хиперболата).

4. От уравнението (11.9) на хиперболата се вижда, че когато се увеличава, тогава тя също нараства. Това следва от факта, че разликата запазва постоянна стойност, равна на единица.

От казаното следва, че хиперболата има формата, показана на фигура 54 (крива, състояща се от два неограничени клона).

Асимптоти на хипербола

Правата L се нарича асимптота на неограничена крива K, ако разстоянието d от точка M на кривата K до тази линия клони към нула, тъй като точката M се движи по кривата K неограничено от началото. Фигура 55 илюстрира концепцията за асимптота: правата L е асимптота за кривата K.

Нека покажем, че хиперболата има две асимптоти:

(11.11)

Тъй като линиите (11.11) и хиперболата (11.9) са симетрични по отношение на координатните оси, достатъчно е да се разгледат само онези точки от посочените линии, които се намират в първия квадрант.

Вземете на права линия точка N със същата абциса x като точка на хипербола (виж Фиг. 56) и намерете разликата ΜN между ординатите на правата линия и клона на хиперболата:

Както можете да видите, с нарастване на x, знаменателят на дробта се увеличава; числителят е постоянна стойност. Следователно дължината на сегмента ΜN клони към нула. Тъй като ΜN е по-голямо от разстоянието d от точката Μ до правата, тогава d още повече клони към нула. Така линиите са асимптоти на хиперболата (11.9).

Когато конструирате хипербола (11.9), препоръчително е първо да конструирате главния правоъгълник на хиперболата (вижте фиг. 57), да начертаете линии, минаващи през противоположните върхове на този правоъгълник - асимптотите на хиперболата и да маркирате върховете и , хипербола .

Уравнението на равностранна хипербола.

чиито асимптоти са координатните оси

Хипербола (11.9) се нарича равностранна, ако нейните полуоси са равни (). Неговото канонично уравнение

(11.12)

Асимптотите на равностранна хипербола имат уравнения и следователно са ъглополовящи на координатните ъгли.

Разгледайте уравнението на тази хипербола в нова координатна система (виж фиг. 58), получена от старата чрез завъртане на координатните оси под ъгъл. Използваме формулите за въртене на координатните оси:

Заменяме стойностите на x и y в уравнение (11.12):

Уравнението на равностранна хипербола, за която осите Ox и Oy са асимптоти, ще има формата .

Още за хиперболата

ексцентричност хипербола (11.9) е съотношението на разстоянието между фокусите към стойността на реалната ос на хиперболата, обозначена с ε:

Тъй като за хипербола , ексцентрицитетът на хиперболата е по-голям от едно: . Ексцентричността характеризира формата на хипербола. Наистина, от равенството (11.10) следва, че т.е. и .

Това показва, че колкото по-малък е ексцентрицитетът на хиперболата, толкова по-малко е съотношението на нейните полуоси, което означава, че толкова повече е удължен главният й правоъгълник.

Ексцентрицитетът на равностранна хипербола е . Наистина ли,

Фокални радиуси и за точките на десния клон на хиперболата имат формата и , а за левия - и .

Правите се наричат ​​директриси на хипербола. Тъй като за хиперболата ε > 1, тогава . Това означава, че дясната директриса е разположена между центъра и десния връх на хиперболата, лявата директриса е между центъра и левия връх.

Директрисите на хипербола имат същото свойство като директрисите на елипса.

Кривата, определена от уравнението, също е хипербола, чиято реална ос 2b е разположена на оста Oy, а въображаемата ос 2 а- по оста Ох. На фигура 59 е показано като пунктирана линия.

Очевидно хиперболите и имат общи асимптоти. Такива хиперболи се наричат ​​спрегнати.

11.5. Парабола

Уравнение на канонична парабола

Парабола е набор от всички точки в равнина, всяка от които е на еднакво разстояние от дадена точка, наречена фокус, и дадена права, наречена директриса. Разстоянието от фокуса F до директрисата се нарича параметър на параболата и се обозначава с p (p> 0).

За да изведем уравнението на параболата, избираме координатната система Oxy така, че оста Oxy да минава през фокуса F перпендикулярно на директрисата в посока от директрисата към F, а началото O да се намира в средата между фокуса и директрисата (виж Фиг. 60). В избраната система фокусът F има координати , а уравнението на директрисата има формата , или .

1. В уравнение (11.13) променливата y е включена в четна степен, което означава, че параболата е симетрична спрямо оста Ox; оста x е оста на симетрия на параболата.

2. Тъй като ρ > 0, от (11.13) следва, че . Следователно параболата е разположена вдясно от оста y.

3. Когато имаме y \u003d 0. Следователно параболата минава през началото.

4. При неограничено нарастване на x, модулът y също нараства неограничено. Параболата има формата (формата), показана на фигура 61. Точката O (0; 0) се нарича връх на параболата, сегментът FM \u003d r се нарича фокален радиус на точката M.

Уравнения , , ( p>0) също дефинират параболи, те са показани на фигура 62

Лесно е да се покаже, че графиката на квадратен трином, където , B и C са реални числа, е парабола в смисъла на нейната дефиниция по-горе.

11.6. Общо уравнение на линии от втори ред

Уравнения на криви от втори ред с оси на симетрия, успоредни на координатните оси

Нека първо намерим уравнението на елипса с център в точка, чиито оси на симетрия са успоредни на координатните оси Ox и Oy, а полуосите са съответно равни на аи b. Нека поставим в центъра на елипсата O 1 началото на новата координатна система , чиито оси и полуоси аи b(вижте фиг. 64):

И накрая, параболите, показани на фигура 65, имат съответните уравнения.

Уравнението

Уравненията на елипса, хипербола, парабола и уравнението на окръжност след трансформации (отворени скоби, преместване на всички членове на уравнението в една посока, въвеждане на подобни членове, въвеждане на нова нотация за коефициентите) могат да бъдат записани с помощта на едно уравнение на формата

където коефициентите A и C не са равни на нула едновременно.

Възниква въпросът: дали някое уравнение от вида (11.14) определя една от кривите (окръжност, елипса, хипербола, парабола) от втори ред? Отговорът се дава от следната теорема.

Теорема 11.2. Уравнение (11.14) винаги дефинира: или кръг (за A = C), или елипса (за A C > 0), или хипербола (за A C< 0), либо параболу (при А×С= 0). При этом возможны случаи вырождения: для эллипса (окружности) - в точку или мнимый эллипс (окружность), для гиперболы - в пару пересекающихся прямых, для параболы - в пару параллельных прямых.

Общо уравнение от втори ред

Помислете сега за общото уравнение от втора степен с две неизвестни:

Различава се от уравнение (11.14) по наличието на член с произведението на координатите (B¹ 0). Възможно е чрез завъртане на координатните оси под ъгъл a да се трансформира това уравнение така, че членът с произведението на координатите да отсъства в него.

Използване на формули за въртене на оси

Нека изразим старите координати чрез новите:

Избираме ъгъл a така, че коефициентът при x "y" да изчезне, т.е. така че равенството

По този начин, когато осите се завъртят под ъгъл a, който удовлетворява условието (11.17), уравнение (11.15) се свежда до уравнение (11.14).

Заключение: общото уравнение от втори ред (11.15) определя на равнината (с изключение на случаите на израждане и разпад) следните криви: окръжност, елипса, хипербола, парабола.

Забележка: Ако A = C, тогава уравнение (11.17) губи смисъла си. В този случай cos2α = 0 (виж (11.16)), тогава 2α = 90°, т.е. α = 45°. Така че, при A = C, координатната система трябва да се завърти на 45 °.

Определение 7.1.Множеството от всички точки на равнината, за които сумата от разстоянията до две фиксирани точки F 1 и F 2 е дадена константа, се нарича елипса.

Определението за елипса дава следния начин за нейното геометрично конструиране. Фиксираме две точки F 1 и F 2 на равнината и означаваме неотрицателна постоянна стойност с 2a. Нека разстоянието между точките F 1 и F 2 е равно на 2c. Представете си, че неразтеглив конец с дължина 2а е фиксиран в точки F 1 и F 2, например, с помощта на две игли. Ясно е, че това е възможно само при a ≥ c. Издърпвайки конеца с молив, начертайте линия, която ще бъде елипса (фиг. 7.1).

Така че описаното множество не е празно, ако a ≥ c. Когато a = c, елипсата е отсечка с краища F 1 и F 2, а когато c = 0, т.е. ако фиксираните точки, посочени в дефиницията на елипса съвпадат, това е окръжност с радиус a. Като отхвърлим тези изродени случаи, ние ще приемем, като правило, че a > c > 0.

Фиксираните точки F 1 и F 2 в дефиниция 7.1 на елипсата (виж фиг. 7.1) се наричат трикове с елипса, разстоянието между тях, означено с 2c, - фокусно разстояние, и сегментите F 1 M и F 2 M, свързващи произволна точка M от елипсата с нейните фокуси, - фокусни радиуси.

Формата на елипсата се определя изцяло от фокусното разстояние |F 1 F 2 | = 2с и параметър a, а положението му в равнината - от двойка точки F 1 и F 2 .

От дефиницията на елипса следва, че тя е симетрична спрямо права линия, минаваща през фокусите F 1 и F 2, както и спрямо права линия, която разделя сегмента F 1 F 2 наполовина и е перпендикулярна на нея (фиг. 7.2, а). Тези линии се наричат оси на елипса. Точката О на тяхното пресичане е центърът на симетрия на елипсата и се нарича центъра на елипсата, и точките на пресичане на елипсата с осите на симетрия (точки A, B, C и D на фиг. 7.2, а) - върховете на елипсата.

Числото а се нарича голяма полуос на елипса, и b = √ (a 2 - c 2) - неговото полумалка ос. Лесно се вижда, че за c > 0, голямата полуос a е равна на разстоянието от центъра на елипсата до тези от нейните върхове, които са на същата ос като фокусите на елипсата (върховете A и B на фиг. 7.2, a), а малката полуос b е равна на разстоянието от централната елипса до другите й два върха (върховете C и D на фиг. 7.2, a).

Уравнение на елипса.Да разгледаме някаква елипса в равнината с фокуси в точките F 1 и F 2 , голяма ос 2a. Нека 2c е фокусното разстояние, 2c = |F 1 F 2 |

Избираме правоъгълна координатна система Oxy на равнината, така че нейният произход да съвпада с центъра на елипсата, а фокусите да са на абсцисата(Фиг. 7.2, b). Тази координатна система се нарича канониченза разглежданата елипса и съответните променливи са каноничен.

В избраната координатна система фокусите имат координати F 1 (c; 0), F 2 (-c; 0). Използвайки формулата за разстоянието между точките, записваме условието |F 1 M| + |F 2 M| = 2a в координати:

√((x - c) 2 + y 2) + √((x + c) 2 + y 2) = 2a. (7.2)

Това уравнение е неудобно, защото съдържа два квадратни радикала. Така че нека го трансформираме. Прехвърляме втория радикал в уравнение (7.2) от дясната страна и го повдигаме на квадрат:

(x - c) 2 + y 2 = 4a 2 - 4a√((x + c) 2 + y 2) + (x + c) 2 + y 2 .

След отваряне на скобите и намаляване на подобни членове, получаваме

√((x + c) 2 + y 2) = a + εx

където ε = c/a. Повтаряме операцията за повдигане на квадрат, за да премахнем и втория радикал: (x + c) 2 + y 2 = a 2 + 2εax + ε 2 x 2, или, като се има предвид стойността на въведения параметър ε, (a 2 - c 2 ) x 2 / a 2 + y 2 = a 2 - c 2 . Тъй като a 2 - c 2 = b 2 > 0, тогава

x 2 /a 2 + y 2 /b 2 = 1, a > b > 0. (7.4)

Уравнение (7.4) се удовлетворява от координатите на всички точки, лежащи върху елипсата. Но при извеждането на това уравнение бяха използвани нееквивалентни трансформации на оригиналното уравнение (7.2) - две повдигания на квадрат, които премахват квадратните радикали. Поставянето на квадрат на уравнение е еквивалентно преобразуване, ако и двете му страни съдържат величини с еднакъв знак, но ние не проверихме това в нашите преобразувания.

Може да не проверим еквивалентността на трансформациите, ако вземем предвид следното. Двойка точки F 1 и F 2 , |F 1 F 2 | = 2c, на равнината определя семейство от елипси с фокуси в тези точки. Всяка точка от равнината, с изключение на точките от отсечката F 1 F 2 , принадлежи на някоя елипса от посоченото семейство. В този случай няма две елипси, които да се пресичат, тъй като сумата от фокалните радиуси еднозначно определя конкретна елипса. И така, описаното семейство елипси без пресичане покрива цялата равнина, с изключение на точките от сегмента F 1 F 2 . Да разгледаме набор от точки, чиито координати удовлетворяват уравнение (7.4) с дадена стойност на параметъра a. Може ли това множество да бъде разпределено между няколко елипси? Някои от точките на множеството принадлежат на елипса с голяма полуос a. Нека в това множество има точка, лежаща на елипса с голяма полуос a. Тогава координатите на тази точка се подчиняват на уравнението

тези. уравнения (7.4) и (7.5) имат общи решения. Въпреки това е лесно да се провери дали системата

за ã ≠ a няма решения. За да направите това, достатъчно е да изключите, например, x от първото уравнение:

което след трансформации води до уравнението

без решения за ã ≠ a, защото . И така, (7.4) е уравнението на елипса с голямата полуос a > 0 и малката полуос b = √ (a 2 - c 2) > 0. Нарича се каноничното уравнение на елипсата.

Изглед на елипса.Обсъденият по-горе геометричен метод за конструиране на елипса дава достатъчна представа за външния вид на елипса. Но формата на една елипса също може да бъде изследвана с помощта на нейното канонично уравнение (7.4). Например, като се има предвид y ≥ 0, можете да изразите y по отношение на x: y = b√(1 - x 2 /a 2) и след като разгледате тази функция, да изградите нейната графика. Има и друг начин за конструиране на елипса. Окръжност с радиус a с център в началото на каноничната координатна система на елипсата (7.4) се описва от уравнението x 2 + y 2 = a 2 . Ако се компресира с коефициента a/b > 1 по у-ос, тогава получавате крива, която е описана от уравнението x 2 + (ya / b) 2 \u003d a 2, т.е. елипса.

Забележка 7.1.Ако същата окръжност се компресира с коефициента a/b

Ексцентричност на елипса. Отношението на фокусното разстояние на елипса към нейната голяма ос се нарича ексцентричност на елипсаи се означава с ε. За дадена елипса

канонично уравнение (7.4), ε = 2c/2a = с/a. Ако в (7.4) параметрите a и b са свързани с неравенството a

За c = 0, когато елипсата се превръща в кръг и ε = 0. В други случаи 0

Уравнение (7.3) е еквивалентно на уравнение (7.4), тъй като уравнения (7.4) и (7.2) са еквивалентни. Следователно (7.3) също е уравнение на елипса. Освен това съотношението (7.3) е интересно с това, че дава проста формула без радикали за дължината |F 2 M| един от фокалните радиуси на точката M(x; y) на елипсата: |F 2 M| = a + εx.

Подобна формула за втория фокусен радиус може да се получи от съображения за симетрия или чрез повтаряне на изчисления, при които, преди да се повдигне на квадрат уравнение (7.2), първият радикал се прехвърля в дясната страна, а не вторият. И така, за всяка точка M(x; y) на елипсата (виж Фиг. 7.2)

|F 1 M | = a - εx, |F 2 M| = a + εx, (7.6)

и всяко от тези уравнения е уравнение на елипса.

Пример 7.1.Нека намерим каноничното уравнение на елипса с голяма полуос 5 и ексцентричност 0,8 и го конструираме.

Познавайки голямата полуос на елипсата a = 5 и ексцентричността ε = 0,8, намираме малката й полуос b. Тъй като b = √ (a 2 - c 2) и c = εa = 4, тогава b = √ (5 2 - 4 2) = 3. Така че каноничното уравнение има формата x 2 / 5 2 + y 2 / 3 2 \u003d 1. За да се изгради елипса, е удобно да се начертае правоъгълник, центриран в началото на каноничната координатна система, чиито страни са успоредни на осите на симетрия на елипсата и равни на нейната съответните оси (фиг. 7.4). Този правоъгълник се пресича с

осите на елипсата в нейните върхове A(-5; 0), B(5; 0), C(0; -3), D(0; 3), а самата елипса е вписана в нея. На фиг. 7.4 също показва фокусите F 1.2 (±4; 0) на елипсата.

Геометрични свойства на елипса.Нека пренапишем първото уравнение в (7.6) като |F 1 M| = (а/ε - x)ε. Обърнете внимание, че стойността на a / ε - x за a > c е положителна, тъй като фокусът F 1 не принадлежи на елипсата. Тази стойност е разстоянието до вертикалната права d: x = a/ε от точката M(x; y) вляво от тази права. Уравнението на елипсата може да бъде написано като

|F 1 M|/(а/ε - x) = ε

Това означава, че тази елипса се състои от тези точки M (x; y) на равнината, за които съотношението на дължината на фокусния радиус F 1 M към разстоянието до правата d е постоянна стойност, равна на ε (фиг. 7.5).

Линията d има "двойник" - вертикална линия d", симетрична на d по отношение на центъра на елипсата, която се дава от уравнението x \u003d -a / ε. По отношение на d елипсата е описана по същия начин както по отношение на d. И двата реда d и d" се наричат директриси на елипса. Директриксите на елипсата са перпендикулярни на оста на симетрия на елипсата, върху която са разположени нейните фокуси, и са отделени от центъра на елипсата на разстояние a / ε = a 2 / c (виж фиг. 7.5).

Разстоянието p от директрисата до най-близкия до нея фокус се нарича фокусен параметър на елипсата. Този параметър е равен на

p \u003d a / ε - c \u003d (a 2 - c 2) / c \u003d b 2 / c

Елипсата има още едно важно геометрично свойство: фокалните радиуси F 1 M и F 2 M сключват равни ъгли с допирателната към елипсата в точка M (фиг. 7.6).

Това свойство има ясно физическо значение. Ако източник на светлина е поставен във фокуса F 1, тогава лъчът, излизащ от този фокус, след отражение от елипсата, ще премине по втория фокусен радиус, тъй като след отражението той ще бъде под същия ъгъл спрямо кривата, както преди отражението . Така всички лъчи, излизащи от фокуса F 1, ще бъдат концентрирани във втория фокус F 2 и обратно. Въз основа на това тълкуване това свойство се нарича оптично свойство на елипса.

Линии от втори ред.
Елипса и нейното канонично уравнение. кръг

След задълбочено проучване прави линии в равнинатание продължаваме да изучаваме геометрията на двуизмерния свят. Залогът е удвоен и ви каня да посетите живописната галерия от елипси, хиперболи, параболи, които са типични представители на линии от втори ред. Обиколката вече започна и първо кратка информация за цялата изложба на различните етажи на музея:

Концепцията за алгебрична права и нейния ред

Права на равнина се нарича алгебричен, ако в афинна координатна системанеговото уравнение има формата , където е полином, състоящ се от членове на формата ( е реално число, са неотрицателни цели числа).

Както можете да видите, уравнението на алгебрична линия не съдържа синуси, косинуси, логаритми и друг функционален бомонд. Само "x" и "y" в цяло число неотрицателностепени.

Ред на линияе равна на максималната стойност на включените в него условия.

Съгласно съответната теорема концепцията за алгебрична линия, както и нейният ред, не зависят от избора афинна координатна система, следователно, за улеснение, считаме, че всички последващи изчисления се извършват в Декартови координати.

Общо уравнениелинията от втори ред има формата , където са произволни реални числа (обичайно е да се пише с множител - "две"), а коефициентите не са едновременно равни на нула.

Ако , тогава уравнението се опростява до , и ако коефициентите не са едновременно равни на нула, тогава това е точно общо уравнение на "плоска" права линия, което представлява първа линия за поръчка.

Мнозина разбраха значението на новите термини, но въпреки това, за да усвоим 100% материала, ние пъхаме пръстите си в гнездото. За да определите реда на реда, повторете всички условиянеговите уравнения и за всяко от тях намерете сбор от мощностивходящи променливи.

Например:

терминът съдържа "x" на 1-ва степен;
терминът съдържа "Y" на 1-ва степен;
няма променливи в термина, така че сумата от техните степени е нула.

Сега нека разберем защо уравнението определя правата второпоръчка:

терминът съдържа "x" на 2-ра степен;
терминът има сумата от степените на променливите: 1 + 1 = 2;
терминът съдържа "у" на 2-ра степен;
всички други условия - по-малъкстепен.

Максимална стойност: 2

Ако добавим допълнително към нашето уравнение, да речем, тогава то вече ще определи линия от трети ред. Очевидно е, че общата форма на уравнението на линията от 3-ти ред съдържа „пълен набор“ от членове, сумата от степени на променливи, в които е равна на три:
, където коефициентите не са едновременно равни на нула.

В случай, че се добавят един или повече подходящи термини, които съдържат , тогава ще говорим за Линии от 4-ти реди т.н.

Ще трябва да се занимаваме с алгебрични линии от 3-ти, 4-ти и по-високи порядъци повече от веднъж, по-специално, когато се запознаваме с полярна координатна система.

Нека обаче се върнем към общото уравнение и си припомним неговите най-прости училищни варианти. Примери за това са параболата, чието уравнение може лесно да се сведе до общ вид, и хиперболата с еквивалентно уравнение. Не всичко обаче е толкова гладко....

Съществен недостатък на общото уравнение е, че почти винаги не е ясно коя права определя. Дори в най-простия случай няма да разберете веднага, че това е хипербола. Такива оформления са добри само при маскарад, следователно в хода на аналитичната геометрия се разглежда типичен проблем редуциране на уравнението на правата от 2-ри ред до каноничната форма.

Каква е каноничната форма на уравнение?

Това е общоприетата стандартна форма на уравнението, когато за секунди става ясно какъв геометричен обект определя. В допълнение, каноничната форма е много удобна за решаване на много практически проблеми. Така, например, според каноничното уравнение "плоска" права, първо, веднага става ясно, че това е права линия, и второ, точката, принадлежаща към нея, и векторът на посоката са просто видими.

Очевидно, всякакви 1-ва линия за поръчкапредставлява права линия. На втория етаж вече не ни чака портиер, а много по-разнообразна компания от девет статуи:

Класификация на линии от втори ред

С помощта на специален набор от действия всяко уравнение на линия от втори ред се свежда до един от следните типове:

(и са положителни реални числа)

1) е каноничното уравнение на елипсата;

2) е каноничното уравнение на хиперболата;

3) е каноничното уравнение на параболата;

4) – въображаемелипса;

5) - двойка пресичащи се линии;

6) - двойка въображаемпресичащи се линии (с единствената реална пресечна точка в началото);

7) - двойка успоредни линии;

8) - двойка въображаемпаралелни линии;

9) е двойка съвпадащи линии.

Някои читатели може да останат с впечатлението, че списъкът е непълен. Например в параграф номер 7 уравнението определя двойката директен, успоредна на оста, и възниква въпросът: къде е уравнението, което определя правите, успоредни на оста y? Отговор: то не се смята за канон. Правите линии представляват същия стандартен случай, завъртян на 90 градуса, а допълнителният запис в класификацията е излишен, тъй като не носи нищо принципно ново.

По този начин има девет и само девет различни типа линии от 2-ри ред, но на практика най-често срещаните са елипса, хипербола и парабола.

Нека първо да разгледаме елипсата. Както обикновено, аз се съсредоточавам върху тези точки, които са от голямо значение за решаването на задачи, и ако имате нужда от подробно извеждане на формули, доказателства на теореми, моля, обърнете се към учебника на Базилев / Атанасян или Александров.

Елипса и нейното канонично уравнение

Правопис ... моля, не повтаряйте грешките на някои потребители на Yandex, които се интересуват от "как да се изгради елипса", "разликата между елипса и овал" и "елебс ексцентричност".

Каноничното уравнение на елипса има формата , където са положителни реални числа и . Ще формулирам дефиницията на елипса по-късно, но засега е време да си починем от приказките и да решим общ проблем:

Как да изградим елипса?

Да, вземете го и просто го нарисувайте. Заданието е често срещано и значителна част от учениците не се справят съвсем компетентно с рисунката:

Пример 1

Построете елипса, дадена от уравнението

Решение: първо привеждаме уравнението в каноничната форма:

Защо да донесе? Едно от предимствата на каноничното уравнение е, че ви позволява незабавно да определите върхове на елипса, които са в точките . Лесно се вижда, че координатите на всяка от тези точки удовлетворяват уравнението .

В такъв случай :


Линеен сегментНаречен главна оселипса;
линейна отсечка – второстепенна ос;
номер Наречен голяма полуоселипса;
номер – полумалка ос.
в нашия пример: .

За да си представите бързо как изглежда тази или онази елипса, просто погледнете стойностите на "a" и "be" на нейното канонично уравнение.

Всичко е наред, спретнато и красиво, но има едно предупреждение: завърших рисунката с помощта на програмата. И можете да рисувате с всяко приложение. В суровата реалност обаче на масата лежи кариран лист хартия, а около ръцете ни танцуват мишки. Хората с артистичен талант, разбира се, могат да спорят, но има и мишки (макар и по-малки). Не напразно човечеството е изобретило линийка, пергел, транспортир и други прости уреди за чертане.

Поради тази причина е малко вероятно да успеем да начертаем точно елипса, знаейки само върховете. Все пак е добре, ако елипсата е малка, например с полуоси. Като алтернатива можете да намалите мащаба и съответно размерите на чертежа. Но в общия случай е много желателно да се намерят допълнителни точки.

Има два подхода за построяване на елипса - геометричен и алгебричен. Не обичам да строя с пергел и линийка поради краткия алгоритъм и значителната бъркотия на чертежа. В случай на спешност, моля, обърнете се към учебника, но в действителност е много по-рационално да използвате инструментите на алгебрата. От уравнението на елипсата в черновата бързо изразяваме:

След това уравнението се разделя на две функции:
– определя горната дъга на елипсата;
– определя долната дъга на елипсата.

Елипса, дадена от каноничното уравнение, е симетрична по отношение на координатните оси, както и по отношение на началото. И това е страхотно - симетрията почти винаги е предвестник на безплатна. Очевидно е достатъчно да се справим с 1-вата координатна четвърт, така че имаме нужда от функция . Предлага намиране на допълнителни точки с абсцисите . Ударихме три SMS-а на калкулатора:

Разбира се, също така е приятно, че ако се направи сериозна грешка в изчисленията, това веднага ще стане ясно по време на строителството.

Маркирайте точки на чертежа (червен цвят), симетрични точки на другите дъги (син цвят) и внимателно свържете цялата компания с линия:


По-добре е да нарисувате първоначалната скица тънко и тънко и едва след това да приложите натиск върху молива. Резултатът трябва да е доста прилична елипса. Между другото, бихте ли искали да знаете каква е тази крива?

Дефиниция на елипса. Фокус на елипса и ексцентричност на елипса

Елипса е специален случай на овал. Думата "овал" не трябва да се разбира във филистимския смисъл ("детето нарисува овал" и т.н.). Това е математически термин с подробна формулировка. Целта на този урок не е да разглежда теорията на овалите и различните им видове, на които практически не се обръща внимание в стандартния курс на аналитична геометрия. И в съответствие с по-актуалните нужди веднага преминаваме към строгата дефиниция на елипса:

Елипса- това е множеството от всички точки на равнината, сумата от разстоянията до всяка от които от две дадени точки, т.нар. триковеелипса, е постоянна стойност, числено равна на дължината на голямата ос на тази елипса: .
В този случай разстоянието между фокусите е по-малко от тази стойност: .

Сега ще стане по-ясно:

Представете си, че синята точка се "вози" върху елипса. Така че, без значение коя точка от елипсата вземем, сумата от дължините на сегментите винаги ще бъде една и съща:

Нека се уверим, че в нашия пример стойността на сумата наистина е равна на осем. Мислено поставете точката "em" в десния връх на елипсата, след това: , което трябваше да бъде проверено.

Друг начин за начертаване на елипса се основава на определението за елипса. Висшата математика понякога е причина за напрежение и стрес, така че е време за поредната сесия на разтоварване. Моля, вземете лист хартия или голям лист картон и го закрепете на масата с два пирона. Това ще са трикове. Завържете зелен конец към стърчащите глави на ноктите и го издърпайте докрай с молив. Върхът на молива ще бъде в някаква точка, която принадлежи на елипсата. Сега започнете да насочвате молива през листа хартия, като държите зеления конец много опънат. Продължете процеса, докато се върнете в началната точка ... отлично ... рисунката може да бъде изпратена за проверка от лекаря на учителя =)

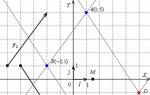
Как да намерим фокуса на елипса?

В горния пример изобразих "готови" фокусни точки и сега ще научим как да ги извличаме от дълбините на геометрията.

Ако елипсата е дадена от каноничното уравнение, тогава нейните фокуси имат координати , къде е разстояние от всеки от фокусите до центъра на симетрия на елипсата.

Изчисленията са по-лесни от задушената ряпа:

! Със значението "ce" е невъзможно да се идентифицират конкретните координати на трикове!Повтарям, това е РАЗСТОЯНИЕ от всеки фокус до центъра(който в общия случай не е задължително да се намира точно в началото).
И следователно разстоянието между фокусите също не може да бъде обвързано с каноничното положение на елипсата. С други думи, елипсата може да бъде преместена на друго място и стойността ще остане непроменена, докато фокусите естествено ще променят своите координати. Моля, имайте предвид това, докато проучвате по-нататък темата.

Ексцентричността на елипсата и нейното геометрично значение

Ексцентричността на елипса е съотношение, което може да приема стойности в рамките на .

В нашия случай:

Нека да разберем как формата на елипсата зависи от нейния ексцентричност. За това фиксирайте левия и десния върхна разглежданата елипса, тоест стойността на голямата полуос ще остане постоянна. Тогава формулата за ексцентричност ще приеме формата: .

Нека започнем да приближаваме стойността на ексцентричността до единица. Това е възможно само ако. Какво означава? ...запомняне на трикове . Това означава, че фокусите на елипсата ще се "разпръснат" по абсцисната ос към страничните върхове. И тъй като „зелените сегменти не са гумени“, елипсата неизбежно ще започне да се изравнява, превръщайки се във все по-тънка и по-тънка наденица, нанизана на ос.

По този начин, колкото по-близък е ексцентрицитетът на елипсата до единица, толкова по-продълговата е елипсата.

Сега нека симулираме обратния процес: фокусите на елипсата тръгнаха един към друг, приближавайки се до центъра. Това означава, че стойността на "ce" намалява и съответно ексцентричността клони към нула: .
В този случай „зелените сегменти“, напротив, ще „се претъпкат“ и ще започнат да „бутат“ линията на елипсата нагоре и надолу.

По този начин, колкото по-близка е стойността на ексцентричността до нула, толкова по-подобна е елипсата... погледнете ограничаващия случай, когато огнищата са успешно обединени отново в началото:

Кръгът е частен случай на елипса

Наистина, в случай на равенство на полуосите, каноничното уравнение на елипсата приема формата, която рефлексивно се трансформира в добре познатото уравнение на кръга от училището с център в началото на радиуса "а".

На практика по-често се използва обозначението с „говорещата“ буква „er“:. Радиусът се нарича дължината на сегмента, докато всяка точка на окръжността се отстранява от центъра с разстоянието на радиуса.

Обърнете внимание, че определението за елипса остава напълно правилно: фокусите съвпадат и сумата от дължините на съвпадащите сегменти за всяка точка от окръжността е постоянна стойност. Тъй като разстоянието между фокусите е ексцентричността на всеки кръг е нула.

Кръг се изгражда лесно и бързо, достатъчно е да се въоръжите с компас. Понякога обаче е необходимо да разберете координатите на някои от неговите точки, в този случай вървим по познатия начин - привеждаме уравнението до веселата форма на Матан:

е функцията на горния полукръг;
е функцията на долния полукръг.

След това намираме желаните стойности, диференцируеми, интегрирами прави други добри неща.

Статията, разбира се, е само за справка, но как може човек да живее без любов в света? Творческа задача за самостоятелно решаване

Пример 2

Съставете каноничното уравнение на елипса, ако са известни един от нейните фокуси и малката полуос (центърът е в началото). Намерете върхове, допълнителни точки и начертайте линия върху чертежа. Изчислете ексцентрицитета.

Решение и рисунка в края на урока

Нека добавим действие:

Завъртете и преместете елипса

Нека се върнем към каноничното уравнение на елипсата, а именно към условието, чиято загадка измъчва любознателните умове от първото споменаване на тази крива. Тук разгледахме елипса , но на практика не може уравнението ? Все пак и тук изглежда като елипса!

Такова уравнение е рядко, но се среща. И наистина дефинира елипса. Нека разсеем мистиката:

В резултат на конструкцията се получава нашата родна елипса, завъртяна на 90 градуса. Това е, - това е неканоничен записелипса . запис!- уравнението не определя никаква друга елипса, тъй като няма точки (фокуси) на оста, които да отговарят на определението за елипса.

Лекции по алгебра и геометрия. Семестър 1.

Лекция 15. Елипса.

Глава 15

т.1. Основни определения.

Определение. Елипса е GMT ​​на равнина, чиято сума от разстоянията до две фиксирани точки на равнината, наречени фокуси, е постоянна стойност.

Определение. Разстоянието от произволна точка M на равнината до фокуса на елипсата се нарича фокален радиус на точката M.

Обозначения:
са фокусите на елипсата,
са фокалните радиуси на точка М.

По дефиниция на елипса, точка M е точка на елипсата тогава и само ако
е постоянна стойност. Тази константа обикновено се означава като 2a:

. (1)

забележи това
.

По дефиниция на елипса, нейните фокуси са фиксирани точки, така че разстоянието между тях също е постоянна стойност за дадената елипса.

Определение. Разстоянието между фокусите на елипса се нарича фокусно разстояние.

Обозначаване:
.

От триъгълник
следва това
, т.е.

.

Означаваме с b числото, равно на
, т.е.

. (2)

Определение. Поведение

(3)

се нарича ексцентричност на елипсата.

Нека въведем координатна система на дадената равнина, която ще наречем канонична за елипсата.

Определение. Оста, върху която лежат фокусите на елипсата, се нарича фокална ос.

Нека конструираме каноничния PDSC за елипсата, вижте фиг.2.

Избираме фокалната ос като абсцисната ос и начертаваме ординатната ос през средата на сегмента
перпендикулярно на фокалната ос.

Тогава огнищата имат координати
,
.

т.2. Канонично уравнение на елипса.

Теорема. В каноничната координатна система за елипса уравнението на елипсата има формата:

. (4)

Доказателство. Ще извършим доказването на два етапа. На първия етап ще докажем, че координатите на всяка точка, разположена върху елипсата, удовлетворяват уравнение (4). На втория етап ще докажем, че всяко решение на уравнение (4) дава координатите на точка, лежаща върху елипсата. Оттук следва, че уравнение (4) се удовлетворява от тези и само онези точки от координатната равнина, които лежат на елипсата. От тук и от дефиницията на уравнението на кривата ще следва, че уравнение (4) е уравнение на елипса.

1) Нека точката M(x, y) е точка на елипсата, т.е. сумата от неговите фокусни радиуси е 2a:

.

Използваме формулата за разстоянието между две точки в координатната равнина и намираме фокалните радиуси на дадена точка M, използвайки тази формула:

,
, откъдето получаваме:

Нека преместим един корен от дясната страна на равенството и го повдигнем на квадрат:

Намалявайки, получаваме:

Даваме подобни, намаляваме с 4 и изолираме радикала:

.

Ние квадрат

Отворете скобите и съкратете
:

откъде получаваме:

Използвайки равенство (2), получаваме:

.

Разделяне на последното равенство на
, получаваме равенство (4), п.т.д.

2) Нека сега двойка числа (x, y) удовлетворява уравнение (4) и нека M(x, y) е съответната точка в координатната равнина Oxy.

Тогава от (4) следва:

.

Заместваме това равенство в израза за фокалните радиуси на точката M:

.

Тук сме използвали равенство (2) и (3).

По този начин,
. по същия начин,
.

Сега отбележете, че от равенството (4) следва, че

или
и защото
, то следва следното неравенство:

.

От това на свой ред следва, че

или
и

,
. (5)

От равенства (5) следва, че
, т.е. точката M(x, y) е точка от елипсата и т.н.

Теоремата е доказана.

Определение. Уравнение (4) се нарича канонично уравнение на елипсата.

Определение. Каноничните координатни оси за елипсата се наричат ​​главни оси на елипсата.

Определение. Началото на каноничната координатна система за елипса се нарича център на елипсата.

т.3. Свойства на елипса.

Теорема. (Свойства на елипса.)

1. В каноничната координатна система за елипсата всички

точките на елипсата са в правоъгълника

,
.

2. Точки лежат върху

3. Елипса е крива, симетрична около

основните им оси.

4. Центърът на елипсата е нейният център на симетрия.

Доказателство. 1, 2) Непосредствено следва от каноничното уравнение на елипсата.

3, 4) Нека M(x, y) е произволна точка от елипсата. Тогава неговите координати удовлетворяват уравнение (4). Но тогава координатите на точките също удовлетворяват уравнение (4) и следователно са точките на елипсата, от която следват твърденията на теоремата.

Теоремата е доказана.

Определение. Величината 2а се нарича голяма ос на елипсата, а величината а се нарича голяма полуос на елипсата.

Определение. Величината 2b се нарича малка ос на елипсата, величината b се нарича малка полуос на елипсата.

Определение. Пресечните точки на елипсата с нейните главни оси се наричат ​​върхове на елипса.

Коментирайте. Една елипса може да бъде конструирана по следния начин. В самолет ние „забиваме пирон“ в триковете и закрепваме нишка с дължина към тях
. След това вземаме молив и с него опъваме конеца. След това преместваме оловото на молива по равнината, като се уверяваме, че конецът е в опънато състояние.

От определението за ексцентричност следва, че

Фиксираме число a и нека c клони към нула. След това при
,
и
. В лимита, който получаваме

или
е уравнението на кръга.

Нека се стремим сега
. Тогава
,
и виждаме, че в границата елипсата се изражда в отсечка
в обозначението на фигура 3.

т.4. Параметрични уравнения на елипса.

Теорема. Позволявам
са произволни реални числа. След това системата от уравнения

,
(6)

са параметричните уравнения на елипсата в каноничната координатна система за елипсата.

Доказателство. Достатъчно е да се докаже, че системата от уравнения (6) е еквивалентна на уравнение (4), т.е. те имат еднакъв набор от решения.

1) Нека (x, y) е произволно решение на система (6). Разделете първото уравнение на a, второто на b, повдигнете двете уравнения на квадрат и добавете:

.

Тези. всяко решение (x, y) на система (6) удовлетворява уравнение (4).

2) Обратно, нека двойката (x, y) е решение на уравнение (4), т.е.

.

От това равенство следва, че точката с координати
лежи върху окръжност с единичен радиус с център в началото, т.е. е точка от тригонометричната окръжност, която съответства на някакъв ъгъл
:

От определението за синус и косинус веднага следва това

,
, където
, откъдето следва, че двойката (x, y) е решение на система (6) и т.н.

Теоремата е доказана.

Коментирайте. Елипса може да се получи в резултат на равномерно "компресиране" на окръжност с радиус a спрямо абсцисната ос.

Позволявам
е уравнението на окръжност с център в началото. "Компресирането" на кръга към абсцисната ос не е нищо повече от трансформация на координатната равнина, извършена съгласно следното правило. На всяка точка M(x, y) поставяме в съответствие точка от същата равнина
, където
,
е коефициентът на "компресия".

С тази трансформация всяка точка от окръжността "преминава" в друга точка от равнината, която има същата абциса, но по-малка ордината. Нека изразим старата ордината на точката чрез новата:

и заменете в уравнението на кръга:

.

От тук получаваме:

. (7)

От това следва, че ако преди трансформацията "компресия" точката M(x, y) лежеше върху окръжността, т.е. нейните координати отговаряха на уравнението на кръга, след което след трансформацията на "компресията" тази точка "премина" в точката
, чиито координати удовлетворяват уравнението на елипсата (7). Ако искаме да получим уравнението на елипса с малка полуос b, тогава трябва да вземем коефициента на компресия

.

т.5. Допирателна към елипса.

Теорема. Позволявам
- произволна точка на елипсата

.

Тогава уравнението на допирателната към тази елипса в точката
изглежда като:

. (8)

Доказателство. Достатъчно е да разгледаме случая, когато точката на допиране лежи в първата или втората четвърт на координатната равнина:
. Уравнението на елипсата в горната полуравнина има формата:

. (9)

Нека използваме уравнението на допирателната към графиката на функцията
в точката
:

където
е стойността на производната на тази функция в точката
. Елипса в първата четвърт може да се разглежда като графика на функция (8). Нека намерим неговата производна и нейната стойност в точката на контакт:

,

. Тук сме се възползвали от факта, че допирната точка
е точка от елипсата и следователно нейните координати удовлетворяват уравнението на елипсата (9), т.е.

.

Заместваме намерената стойност на производната в уравнението на допирателната (10):

,

откъде получаваме:

Това предполага:

Нека разделим това уравнение на
:

.

Остава да отбележим, че
, защото точка
принадлежи на елипсата и нейните координати удовлетворяват нейното уравнение.

Уравнението на допирателната (8) се доказва по подобен начин в допирателната точка, разположена в третата или четвъртата четвърт на координатната равнина.

И накрая, можем лесно да видим, че уравнение (8) дава уравнението на допирателната в точките
,
:

или
, и
или
.

Теоремата е доказана.

т.6. Огледалното свойство на елипса.

Теорема. Допирателната към елипсата има равни ъгли с фокалните радиуси на допирателната точка.

Позволявам
- точка на допир
,
са фокалните радиуси на допирателната точка, P и Q са проекциите на фокусите върху допирателната, начертана към елипсата в точката
.

Теоремата гласи, че

. (11)

Това равенство може да се тълкува като равенство на ъглите на падане и отражение на светлинен лъч от елипса, освободена от нейния фокус. Това свойство се нарича огледално свойство на елипсата:

Светлинен лъч, излъчен от фокуса на елипсата, след отражение от огледалото на елипсата, преминава през друг фокус на елипсата.

Доказателство на теоремата. За да докажем равенството на ъглите (11), доказваме сходството на триъгълниците
и
, в която страните
и
ще бъде подобен. Тъй като триъгълниците са правоъгълни, достатъчно е да се докаже равенството

Определение. Елипса е геометричното място на точки в равнина, сумата от разстоянията на всяка от тях от две дадени точки от тази равнина, наречени фокуси, е постоянна стойност (при условие, че тази стойност е по-голяма от разстоянието между фокусите).

Нека означим фокусите чрез разстоянието между тях - през , и постоянна стойност, равна на сумата от разстоянията от всяка точка на елипсата до фокусите, през (по условие ).

Нека изградим декартова координатна система, така че фокусите да са на абсцисната ос, а началото на координатите да съвпада със средата на сегмента (фиг. 44). Тогава фокусите ще имат следните координати: ляв фокус и десен фокус. Нека изведем уравнението на елипсата в координатната система, която сме избрали. За тази цел разгледайте произволна точка от елипсата. По дефиницията на елипса сумата от разстоянията от тази точка до фокусите е:

Използвайки формулата за разстоянието между две точки, получаваме следователно

За да опростим това уравнение, ние го записваме във формата

Тогава повдигането на квадрат на двете страни на уравнението дава

или след очевидни опростявания:

Сега отново повдигаме на квадрат двете страни на уравнението, след което ще имаме:

или след идентични трансформации:

Тъй като според условието в дефиницията на елипса , тогава е положително число. Въвеждаме нотацията

Тогава уравнението ще приеме следния вид:

По дефиниция на елипса, координатите на всяка от нейните точки отговарят на уравнение (26). Но уравнение (29) е следствие от уравнение (26). Следователно, той също така удовлетворява координатите на всяка точка от елипсата.

Може да се покаже, че координатите на точки, които не лежат на елипсата, не отговарят на уравнение (29). Така уравнение (29) е уравнение на елипса. Нарича се канонично уравнение на елипсата.

Нека установим формата на елипсата, използвайки нейното канонично уравнение.

Първо, имайте предвид, че това уравнение съдържа само четни степени на x и y. Това означава, че ако която и да е точка принадлежи на елипса, тогава тя също така включва точка, която е симетрична на точка около абсцисната ос, и точка, която е симетрична на точка спрямо оста y. Така елипсата има две взаимно перпендикулярни оси на симетрия, които в избраната от нас координатна система съвпадат с координатните оси. Осите на симетрия на елипсата ще се наричат ​​оси на елипсата, а точката на тяхното пресичане - център на елипсата. Оста, върху която са разположени фокусите на елипсата (в този случай оста на абсцисата), се нарича фокална ос.

Нека определим формата на елипсата първо през първата четвърт. За да направим това, решаваме уравнение (28) по отношение на y:

Очевидно е, че тук, тъй като y приема въображаеми стойности за . С увеличаване от 0 до a, y намалява от b до 0. Частта от елипсата, лежаща в първата четвърт, ще бъде дъга, ограничена от точки B (0; b) и лежаща на координатните оси (фиг. 45). Използвайки сега симетрията на елипсата, заключаваме, че елипсата има формата, показана на фиг. 45.

Пресечните точки на елипсата с осите се наричат ​​върхове на елипсата. От симетрията на елипсата следва, че освен върховете, елипсата има още два върха (виж фиг. 45).

Отсечките и свързващите срещуположните върхове на елипсата, както и техните дължини се наричат ​​съответно голяма и малка ос на елипсата. Числата a и b се наричат ​​съответно голяма и малка полуос на елипсата.

Съотношението на половината от разстоянието между фокусите към голямата полуос на елипсата се нарича ексцентричност на елипсата и обикновено се обозначава с буквата:

Тъй като , тогава ексцентричността на елипсата е по-малка от единица: Ексцентричността характеризира формата на елипсата. Наистина, от формула (28) следва, че от това се вижда, че колкото по-малък е ексцентрицитетът на елипсата, толкова по-малко нейната малка полуос b се различава от голямата полуос a, т.е. колкото по-малко е удължена елипсата (по фокалната ос).

В граничния случай, когато получите кръг с радиус a: , или . В същото време фокусите на елипсата, така да се каже, се сливат в една точка - центъра на кръга. Ексцентричността на окръжността е нула:

Връзката между елипсата и кръга може да се установи и от друга гледна точка. Нека покажем, че елипса с полуоси a и b може да се разглежда като проекция на окръжност с радиус a.

Нека разгледаме две равнини P и Q, образуващи такъв ъгъл a помежду си, за който (фиг. 46). Построяваме координатна система в равнина P и система Oxy в равнина Q с общо начало O и обща абсцисна ос, съвпадаща с пресечната линия на равнините. Да разгледаме кръга в равнината P

с център в началото и радиус a. Нека е произволно избрана точка от окръжността, е нейната проекция върху равнината Q и е проекцията на точката M върху оста Ox. Нека покажем, че точката лежи върху елипса с полуоси a и b.