Намерете детерминантата на оригиналната матрица. Ако детерминантата на матрица е нула, тогава нейната обратна не съществува

Формулиране на проблема

Задачата изисква потребителят да се запознае с основните понятия на числените методи, като детерминанта и обратна матрица, и различни начини за тяхното изчисляване. Този теоретичен доклад първо въвежда основните понятия и дефиниции на прост и достъпен език, въз основа на които се извършват по-нататъшни изследвания. Потребителят може да няма специални познания в областта на числените методи и линейната алгебра, но може лесно да използва резултатите от тази работа. За нагледност е дадена програма за изчисляване на детерминанта на матрица по няколко метода, написана на езика за програмиране C++. Програмата се използва като лабораторен стенд за създаване на илюстрации към доклада. Провежда се и изследване на методи за решаване на системи от линейни алгебрични уравнения. Безполезността на изчисляването на обратната матрица е доказана, така че работата предоставя по-оптимални начини за решаване на уравнения, без да се изчислява. Той обяснява защо има толкова много различни методи за изчисляване на детерминанти и обратни матрици и обсъжда техните недостатъци. Отчитат се и грешките при изчисляване на детерминантата и се оценява постигнатата точност. В допълнение към руските термини, работата използва и техните английски еквиваленти, за да разбере под какви имена да търсите числените процедури в библиотеките и какво означават техните параметри.

Основни определения и най-прости свойства

Определящо

Нека въведем дефиницията на детерминантата на квадратна матрица от произволен ред. Това определение ще бъде рецидивиращ, тоест, за да установите каква е детерминантата на матрицата на подредбата, трябва вече да знаете каква е детерминантата на матрицата на подредбата. Обърнете внимание също, че детерминантата съществува само за квадратни матрици.

Ще обозначим детерминантата на квадратна матрица с или det.

Определение 1. Определящоквадратна матрица извиква се номер на втори ред .

Определящо квадратна матрица от ред , се нарича число

където е детерминантата на матрицата на реда, получена от матрицата чрез изтриване на първия ред и колона с номер.

За по-голяма яснота, нека запишем как можете да изчислите детерминантата на матрица от четвърти ред:

Коментирайте.Действителното изчисляване на детерминантите за матрици над трети ред въз основа на дефиницията се използва в изключителни случаи. Обикновено изчислението се извършва с помощта на други алгоритми, които ще бъдат обсъдени по-късно и които изискват по-малко изчислителна работа.

Коментирайте.В Дефиниция 1 би било по-точно да се каже, че детерминантата е функция, дефинирана върху набор от квадратни матрици от ред и приемащи стойности в набора от числа.

Коментирайте.В литературата вместо понятието „детерминанта“ се използва и понятието „детерминанта“, което има същото значение. От думата „детерминант“ се появява обозначението дет.

Нека разгледаме някои свойства на детерминантите, които ще формулираме под формата на твърдения.

Твърдение 1.При транспониране на матрица детерминантата не се променя, т.е.

Твърдение 2.Детерминантата на произведението на квадратни матрици е равна на произведението на детерминантите на факторите, т.е.

Твърдение 3.Ако два реда в една матрица се разменят, нейният детерминант ще промени знака.

Твърдение 4.Ако една матрица има два еднакви реда, тогава нейният детерминант е нула.

В бъдеще ще трябва да добавяме низове и да умножаваме низ по число. Ще изпълняваме тези действия върху редове (колони) по същия начин, както действията върху матрици на редове (матрици на колони), тоест елемент по елемент. Резултатът ще бъде ред (колона), който по правило не съвпада с редовете на оригиналната матрица. Ако има операции за добавяне на редове (колони) и умножаването им по число, можем да говорим и за линейни комбинации от редове (колони), тоест суми с числови коефициенти.

Твърдение 5.Ако ред от матрица се умножи по число, тогава неговият детерминант ще бъде умножен по това число.

Твърдение 6.Ако една матрица съдържа нулев ред, тогава нейният детерминант е нула.

Твърдение 7.Ако един от редовете на матрицата е равен на друг, умножен по число (редовете са пропорционални), тогава детерминантата на матрицата е равна на нула.

Твърдение 8.Нека i-тият ред в матрицата има формата . Тогава , където матрицата се получава от матрицата чрез заместване на i-тия ред с реда , а матрицата се получава чрез заместване на i-тия ред с реда .

Твърдение 9.Ако добавите друг ред към един от редовете на матрицата, умножен по число, тогава детерминантата на матрицата няма да се промени.

Твърдение 10.Ако един от редовете на матрицата е линейна комбинация от другите й редове, тогава детерминантата на матрицата е равна на нула.

Определение 2. Алгебрично допълнениекъм матричен елемент е число, равно на , където е детерминантата на матрицата, получена от матрицата чрез изтриване на i-тия ред и j-тата колона. Алгебричното допълнение на матричен елемент се означава с .

Пример.Позволявам . Тогава

Коментирайте.Използвайки алгебрични допълнения, дефиницията на 1 детерминанта може да бъде записана по следния начин:

Твърдение 11. Разгъване на детерминантата в произволен низ.

Формулата за детерминанта на матрицата е

Пример.Изчисли .

Решение.Нека използваме разширението по третия ред, това е по-изгодно, тъй като в третия ред две от трите числа са нули. Получаваме

Твърдение 12.За квадратна матрица от ред при , отношението е валидно: .

Твърдение 13.Всички свойства на детерминантата, формулирани за редове (изявления 1 - 11), са валидни и за колони, по-специално декомпозицията на детерминантата в j-тата колона е валидна и равенство при .

Твърдение 14.Детерминантата на триъгълна матрица е равна на произведението на елементите на главния й диагонал.

Последица.Детерминантата на матрицата на идентичност е равна на едно, .

Заключение.Свойствата, изброени по-горе, позволяват да се намерят детерминанти на матрици от достатъчно високи порядки с относително малко количество изчисления. Алгоритъмът за изчисление е както следва.

Алгоритъм за създаване на нули в колона.Да предположим, че трябва да изчислим детерминантата на реда. Ако , тогава разменете първия ред и всеки друг ред, в който първият елемент не е нула. В резултат на това детерминантата , ще бъде равна на детерминантата на новата матрица с обратен знак. Ако първият елемент на всеки ред е равен на нула, тогава матрицата има нулева колона и съгласно твърдения 1, 13 нейният детерминант е равен на нула.

И така, ние вярваме, че вече в оригиналната матрица . Оставяме първия ред непроменен. Добавете към втория ред първия ред, умножен по числото. Тогава първият елемент от втория ред ще бъде равен на .

Означаваме останалите елементи от новия втори ред с , . Детерминантата на новата матрица съгласно твърдение 9 е равна на . Умножете първия ред по число и го добавете към третия. Първият елемент от новия трети ред ще бъде равен на

Означаваме останалите елементи от новия трети ред с , . Детерминантата на новата матрица съгласно твърдение 9 е равна на .

Ще продължим процеса на получаване на нули вместо първите елементи на линиите. Накрая умножете първия ред по число и го добавете към последния ред. Резултатът е матрица, нека я обозначим , която има формата

и . За да изчислим детерминантата на матрицата, използваме разширение в първата колона

От тогава

От дясната страна е детерминантата на матрицата на реда. Прилагаме към него същия алгоритъм и изчисляването на детерминантата на матрицата ще се сведе до изчисляване на детерминантата на матрицата на реда. Повтаряме процеса, докато достигнем детерминанта от втори ред, която се изчислява по дефиниция.

Ако матрицата няма специфични свойства, тогава не е възможно значително да се намали количеството на изчисленията в сравнение с предложения алгоритъм. Друг добър аспект на този алгоритъм е, че е лесно да се използва за създаване на компютърна програма за изчисляване на детерминанти на матрици от големи поръчки. Стандартните програми за изчисляване на детерминанти използват този алгоритъм с незначителни промени, свързани с минимизиране на влиянието на грешки при закръгляване и грешки при въвеждане на данни при компютърни изчисления.

Пример.Изчисляване на детерминанта на матрица .

Решение.Оставяме първия ред непроменен. Към втория ред добавяме първия, умножен по числото:

Детерминантата не се променя. Към третия ред добавяме първия, умножен по числото:

Детерминантата не се променя. Към четвъртия ред добавяме първия, умножен по числото:

Детерминантата не се променя. В резултат на това получаваме

Използвайки същия алгоритъм, изчисляваме детерминантата на матрицата от ред 3, разположена вдясно. Оставяме първия ред непроменен, добавяме първия ред, умножен по числото, към втория ред :

Към третия ред добавяме първия, умножен по числото :

В резултат на това получаваме

Отговор. .

Коментирайте.Въпреки че при изчисленията са използвани дроби, резултатът се оказва цяло число. Наистина, използвайки свойствата на детерминантите и факта, че оригиналните числа са цели числа, операциите с дроби могат да бъдат избегнати. Но в инженерната практика числата изключително рядко са цели числа. Следователно, като правило, елементите на детерминантата ще бъдат десетични дроби и е неуместно да се използват каквито и да било трикове за опростяване на изчисленията.

обратна матрица

Определение 3.Матрицата се нарича обратна матрицаза квадратна матрица, ако .

От дефиницията следва, че обратната матрица ще бъде квадратна матрица от същия ред като матрицата (в противен случай един от продуктите или няма да бъде дефиниран).

Обратната матрица се означава с . Следователно, ако съществува, тогава .

От определението за обратна матрица следва, че матрицата е обратна на матрицата, т.е. Можем да кажем за матриците, че те са обратни една на друга или взаимно обратни.

Ако детерминантата на матрица е нула, тогава нейната обратна не съществува.

Тъй като за намиране на обратната матрица е важно дали детерминантата на матрицата е равна на нула или не, въвеждаме следните определения.

Определение 4.Нека наречем квадратната матрица изродениили специална матрица, ако неизродениили неособена матрица, Ако .

Изявление.Ако обратната матрица съществува, тогава тя е уникална.

Изявление.Ако квадратната матрица е неособена, тогава нейната обратна съществува и (1) където са алгебрични допълнения към елементите.

Теорема.Обратна матрица за квадратна матрица съществува тогава и само ако матрицата е неособена, обратната матрица е уникална и формула (1) е валидна.

Коментирайте.Особено внимание трябва да се обърне на местата, заети от алгебрични добавки във формулата на обратната матрица: първият индекс показва числото колона, а второто е числото линии, в който трябва да напишете изчисленото алгебрично събиране.

Пример. .

Решение.Намиране на определителя

Тъй като , тогава матрицата е неизродена и нейната обратна съществува. Намиране на алгебрични допълнения:

Съставяме обратната матрица, като поставяме намерените алгебрични добавки така, че първият индекс да съответства на колоната, а вторият на реда: (2)

Получената матрица (2) служи като отговор на проблема.

Коментирайте.В предишния пример би било по-точно да напишете отговора така:
(3)

Нотацията (2) обаче е по-компактна и е по-удобно да се извършват допълнителни изчисления с нея, ако е необходимо. Следователно записването на отговора във формата (2) е за предпочитане, ако елементите на матрицата са цели числа. И обратно, ако елементите на матрицата са десетични дроби, тогава е по-добре да напишете обратната матрица без множител отпред.

Коментирайте.Когато намирате обратната матрица, трябва да извършите доста изчисления и правилото за подреждане на алгебрични добавки в крайната матрица е необичайно. Следователно има голяма вероятност за грешка. За да избегнете грешки, трябва да проверите: изчислете произведението на оригиналната матрица и крайната матрица в един или друг ред. Ако резултатът е единична матрица, тогава обратната матрица е намерена правилно. В противен случай трябва да потърсите грешка.

Пример.Намерете обратното на матрица .

Решение. - съществува.

Отговор: .

Заключение.Намирането на обратната матрица с помощта на формула (1) изисква твърде много изчисления. За матрици от четвърти ред и по-висок това е неприемливо. Действителният алгоритъм за намиране на обратната матрица ще бъде даден по-късно.

Изчисляване на детерминанта и обратна матрица по метода на Гаус

Методът на Гаус може да се използва за намиране на детерминанта и обратна матрица.

А именно, детерминантата на матрицата е равна на det.

Обратната матрица се намира чрез решаване на системи от линейни уравнения с помощта на метода на елиминиране на Гаус:

Където е j-тата колона на матрицата за идентичност, е желаният вектор.

Получените вектори на решение очевидно образуват колони на матрицата, тъй като .

Формули за детерминанта

1. Ако матрицата е неособена, тогава и (продукт на водещи елементи).

Дадена е система от N линейни алгебрични уравнения (СЛАУ) с неизвестни, чиито коефициенти са елементите на матрицата, а свободните членове са числа

Първият индекс до коефициентите показва в кое уравнение се намира коефициентът, а вторият - в кое от неизвестните се намира.

Ако матричната детерминанта не е нула

тогава системата от линейни алгебрични уравнения има единствено решение.

Решението на система от линейни алгебрични уравнения е такъв подреден набор от числа, който трансформира всяко от уравненията на системата в правилно равенство.

Ако десните части на всички уравнения на системата са равни на нула, тогава системата от уравнения се нарича хомогенна. В случай, че някои от тях са различни от нула – разнородни

Ако система от линейни алгебрични уравнения има поне едно решение, тогава тя се нарича съвместима, в противен случай се нарича несъвместима.

Ако решението на системата е единствено, тогава системата от линейни уравнения се нарича определена. В случай, че решението на съвместна система не е уникално, системата от уравнения се нарича неопределена.

Две системи от линейни уравнения се наричат ​​еквивалентни (или еквивалентни), ако всички решения на една система са решения на втората и обратно. Получаваме еквивалентни (или еквивалентни) системи, използвайки еквивалентни трансформации.

Еквивалентни трансформации на SLAE

1) пренареждане на уравнения;

2) умножение (или деление) на уравнения с различно от нула число;

3) добавяне на друго уравнение към някое уравнение, умножено по произволно различно от нула число.

Решението на SLAE може да бъде намерено по различни начини.

МЕТОД НА КРАМЕР

ТЕОРЕМА НА КРАМЪР. Ако детерминантата на система от линейни алгебрични уравнения с неизвестни е различна от нула, тогава тази система има уникално решение, което се намира с помощта на формулите на Крамер:

— детерминанти, образувани чрез замяна на th колона с колона от свободни членове.

Ако , и поне един от тях е различен от нула, тогава SLAE няма решения. Ако , тогава SLAE има много решения. Нека да разгледаме примери, използващи метода на Cramer.

—————————————————————

Дадена е система от три линейни уравнения с три неизвестни. Решете системата с помощта на метода на Крамер

Нека намерим детерминантата на матрицата на коефициента за неизвестни

Тъй като , тогава дадената система от уравнения е последователна и има единствено решение. Нека изчислим детерминантите:

Използвайки формулите на Креймър намираме неизвестните

Така единственото решение на системата.

Дадена е система от четири линейни алгебрични уравнения. Решете системата с помощта на метода на Крамер.

Нека намерим детерминантата на матрицата на коефициента за неизвестните. За да направите това, нека го разширим по първия ред.

Нека намерим компонентите на детерминантата:

Нека заместим намерените стойности в детерминанта

Детерминанта, следователно системата от уравнения е последователна и има единствено решение. Нека изчислим детерминантите с помощта на формулите на Cramer:

Нека разложим всяка от детерминантите според колоната, в която има повече нули.

Използвайки формулите на Креймър намираме

Системно решение

Този пример може да бъде решен с помощта на математически калкулатор YukhymCALC. Фрагмент от програмата и резултатите от изчисленията са показани по-долу.

——————————

МЕТОД НА КРАМЕРА

|1,1,1,1|

D=|5,-3,2,-8|

|3,5,1,4|

|4,2,3,1|

D=1*(-3*1*1+2*4*2+(-8)*5*3-((-8)*1*2+2*5*1+(-3)*4* 3))-1*(5*1*1+2*4*4+(-8)*3*3-((-8)*1*4+2*3*1+5*4*3) )+1*(5*5*1+(-3)*4*4+(-8)*3*2-((-8)*5*4+(-3)*3*1+5* 4*2))-1*(5*1*1+2*4*4+(-8)*3*3-((-8)*1*4+2*3*1+5*4* 3))= 1*(-3+16-120+16-10+36)-1*(5+32-72+32-6-60)+1*(25-48-48+160+9- 40)-1*(75-12+12-40+27-10)=1*(-65)-1*(-69)+1*58-1*52=-65+69+58-52= 10

|0,1,1,1|

Dx1=|1,-3,2,-8|

|0,5,1,4|

|3,2,3,1|

Dx1=-1*(1*1*1+2*4*3+(-8)*0*3-((-8)*1*3+2*0*1+1*4*3)) +1*(1*5*1+(-3)*4*3+(-8)*0*2-((-8)*5*3+(-3)*0*1+1*4 *2))-1*(1*1*1+2*4*3+(-8)*0*3-((-8)*1*3+2*0*1+1*4*3 ))= -1*(1+24+0+24+0-12)+1*(5-36+0+120+0-8)-1*(15-9+0-30+0-2 )= -1*(37)+1*81-1*(-26)=-37+81+26=70

|1,0,1,1|

Dx2=|5,1,2,-8|

|3,0,1,4|

|4,3,3,1|

Dx2=1*(1*1*1+2*4*3+(-8)*0*3-((-8)*1*3+2*0*1+1*4*3))+ 1*(5*0*1+1*4*4+(-8)*3*3-((-8)*0*4+1*3*1+5*4*3))-1* (5*1*1+2*4*4+(-8)*3*3-((-8)*1*4+2*3*1+5*4*3))= 1*(1 +24+0+24+0-12)+1*(0+16-72+0-3-60)-1*(0+4+18+0-9-15)= 1*37+1* (-119)-1*(-2)=37-119+2=-80

|1,1,0,1|

Dx3=|5,-3,1,-8|

|3,5,0,4|

|4,2,3,1|

Dx3=1*(-3*0*1+1*4*2+(-8)*5*3-((-8)*0*2+1*5*1+(-3)*4* 3))-1*(5*0*1+1*4*4+(-8)*3*3-((-8)*0*4+1*3*1+5*4*3) )-1*(5*0*1+1*4*4+(-8)*3*3-((-8)*0*4+1*3*1+5*4*3))= 1*(0+8-120+0-5+36)-1*(0+16-72+0-3-60)-1*(75+0+6-20+27+0)= 1* (-81)-1*(-119)-1*88=-81+119-88=-50

|1,1,1,0|

Dx4=|5,-3,2,1|

|3,5,1,0|

|4,2,3,3|

Dx4=1*(-3*1*3+2*0*2+1*5*3-(1*1*2+2*5*3+(-3)*0*3))-1* (5*1*3+2*0*4+1*3*3-(1*1*4+2*3*3+5*0*3))+1*(5*5*3+( -3)*0*4+1*3*2-(1*5*4+(-3)*3*3+5*0*2))= 1*(-9+0+15-2- 30+0)-1*(15+0+9-4-18+0)+1*(75+0+6-20+27+0)= 1*(-26)-1*(2)+ 1*88=-26-2+88=60

x1=Dx1/D=70.0000/10.0000=7.0000

x2=Dx2/D=-80.0000/10.0000=-8.0000

x3=Dx3/D=-50.0000/10.0000=-5.0000

x4=Dx4/D=60.0000/10.0000=6.0000

Вижте материали:

(jкоментира)

В общия случай правилото за изчисляване на детерминанти на реда е доста тромаво. За детерминанти от втори и трети ред има рационални начини за изчисляването им.

Изчисления на детерминанти от втори ред

За да изчислите детерминантата на матрица от втори ред, трябва да извадите произведението на елементите на вторичния диагонал от произведението на елементите на главния диагонал:

Пример

Упражнение.Изчислете детерминанта от втори ред

Решение.

Отговор.

Методи за изчисляване на детерминанти от трети ред

Съществуват следните правила за изчисляване на детерминанти от трети ред.

Правило на триъгълника

Схематично това правило може да се изобрази по следния начин:

Продуктът на елементите в първата детерминанта, които са свързани с прави линии, се приема със знак плюс; аналогично за втората детерминанта съответните произведения се вземат със знак минус, т.е.

Пример

Упражнение.Изчислителна детерминанта използвайки метода на триъгълника.

Решение.

Отговор.

Правилото на Сарус

Вдясно от определителя се добавят първите две колони и произведенията на елементите по главния диагонал и по успоредните му диагонали се вземат със знак плюс; и произведенията на елементите на вторичния диагонал и диагоналите, успоредни на него, със знак минус:

Пример

Упражнение.Изчислителна детерминанта използвайки правилото на Сарус.

Решение.

Отговор.

Разширяване на детерминантата по ред или колона

Детерминантата е равна на сумата от произведенията на елементите от реда на детерминантата и техните алгебрични допълнения.

Обикновено се избира редът/колоната, който съдържа нули. Редът или колоната, по които се извършва разлагането, ще бъдат обозначени със стрелка.

Пример

Упражнение.Разгънете по първия ред, изчислете детерминантата

Решение.

Отговор.

Този метод позволява изчисляването на детерминантата да се сведе до изчисляване на детерминанта от по-нисък порядък.

Пример

Упражнение.Изчислителна детерминанта

Решение.Нека извършим следните трансформации на редовете на детерминанта: от втория ред изваждаме първите четири, а от третия първия ред, умножен по седем, в резултат на това според свойствата на детерминанта получаваме детерминанта равен на дадения.

Детерминантата е нула, защото вторият и третият ред са пропорционални.

Отговор.

За изчисляване на детерминанти от четвърти ред и по-висок се използва или разширение в ред/колона, или редукция до триъгълна форма, или използване на теоремата на Лаплас.

Разлагане на детерминантата на елементи от ред или колона

Пример

Упражнение.Изчислителна детерминанта , разлагайки го на елементи от някакъв ред или някаква колона.

Решение.Нека първо извършим елементарни трансформации на редовете на детерминанта, като направим възможно най-много нули в реда или в колоната. За да направите това, първо извадете девет трети от първия ред, пет трети от втория и три трети от четвъртия, получаваме:

Нека разложим получената детерминанта на елементите от първата колона:

Също така ще разширим получения детерминант от трети ред в елементите на реда и колоната, като преди това сме получили нули, например в първата колона.

За да направите това, извадете вторите два реда от първия ред и втория ред от третия:

Отговор.

Коментирайте

Последната и предпоследната детерминанти не могат да бъдат изчислени, но веднага се заключава, че са равни на нула, тъй като съдържат пропорционални редове.

Намаляване на детерминантата до триъгълна форма

С помощта на елементарни трансформации над редове или колони детерминантата се редуцира до триъгълна форма и тогава стойността му, според свойствата на детерминантата, е равна на произведението на елементите по главния диагонал.

Пример

Упражнение.Изчислителна детерминанта довеждайки го до триъгълна форма.

Решение.Първо правим нули в първата колона под главния диагонал.

4. Свойства на детерминантите. Детерминанта на произведението на матрици.

Всички трансформации ще бъдат по-лесни за изпълнение, ако елементът е равен на 1. За да направим това, ще разменим първата и втората колона на детерминантата, което според свойствата на детерминантата ще я накара да промени знака си на противоположно:

След това получаваме нули във втората колона на мястото на елементите под главния диагонал. Отново, ако диагоналният елемент е равен на , тогава изчисленията ще бъдат по-прости. За да направите това, разменете втория и третия ред (и в същото време променете на противоположния знак на детерминантата):

Отговор.

Теорема на Лаплас

Пример

Упражнение.Използвайки теоремата на Лаплас, изчислете детерминантата

Решение.Нека изберем два реда в този детерминант от пети ред - втория и третия, тогава получаваме (пропускаме членовете, които са равни на нула):

Отговор.

ЛИНЕЙНИ УРАВНЕНИЯ И НЕРАВЕНСТВА I

§ 31 Случаят, когато основната детерминанта на система от уравнения е равна на нула и поне една от спомагателните детерминанти е различна от нула

Теорема.Ако основната детерминанта на системата от уравнения

(1)

е равно на нула и поне една от спомагателните детерминанти е различна от нула, тогава системата е непоследователна.

Формално, доказателството на тази теорема не е трудно да се получи от противно. Да приемем, че системата от уравнения (1) има решение ( х 0 , г 0). След това, както е показано в предишния параграф,

Δ х 0 = Δ х , Δ г 0 = Δ г (2)

Но според състоянието Δ = 0 и поне една от детерминантите Δ х И Δ г различен от нула. Следователно равенствата (2) не могат да бъдат изпълнени едновременно. Теоремата е доказана.

Въпреки това изглежда интересно да разберем по-подробно защо системата от уравнения (1) е непоследователна в разглеждания случай.

означава, че коефициентите за неизвестните в системата от уравнения (1) са пропорционални. нека например

а 1 =ка 2 ,б 1 = kb 2 .

означава, че коефициентите за при и свободните членове на уравненията на системата (1) не са пропорционални. Тъй като b 1 = kb 2, тогава ° С 1 =/= kc 2 .

Следователно системата от уравнения (1) може да бъде записана в следния вид:

В тази система коефициентите за неизвестните са съответно пропорционални, но коефициентите за при (или кога х ) и безплатните условия не са пропорционални. Такава система, разбира се, е несъвместима. Наистина, ако имаше решение ( х 0 , г 0), тогава числовите равенства ще са валидни

к (а 2 х 0 + b 2 г 0) = ° С 1

а 2 х 0 + b 2 г 0 = ° С 2 .

Но едно от тези равенства противоречи на другото: в крайна сметка, ° С 1 =/= kc 2 .

Разгледахме само случая, когато Δ х =/= 0. Случаят може да се разглежда по подобен начин, когато Δ г =/= 0."

Доказаната теорема може да се формулира по този начин.

Ако коефициентите за неизвестните хИ прив системата от уравнения (1) са пропорционални, но коефициентите за някое от тези неизвестни и свободните членове не са пропорционални, тогава тази система от уравнения е непоследователна.

Лесно е например да се уверите, че всяка от тези системи ще бъде несъвместима:

Метод на Крамер за решаване на системи от линейни уравнения

Формули на Крамер

Методът на Крамър се основава на използването на детерминанти при решаване на системи от линейни уравнения. Това значително ускорява процеса на решение.

Методът на Крамър може да се използва за решаване на система от толкова линейни уравнения, колкото неизвестни има във всяко уравнение.

Методът на Крамер. Приложение за системи от линейни уравнения

Ако детерминантата на системата не е равна на нула, тогава методът на Крамър може да се използва в решението, но ако е равна на нула, тогава не може. В допълнение, методът на Cramer може да се използва за решаване на системи от линейни уравнения, които имат уникално решение.

Определение. Детерминанта, съставена от коефициенти за неизвестни, се нарича детерминанта на системата и се обозначава (делта).

Детерминанти

се получават чрез заместване на коефициентите на съответните неизвестни със свободни членове:

;

.

Теорема на Крамър. Ако детерминантата на системата е различна от нула, тогава системата от линейни уравнения има едно единствено решение и неизвестното е равно на отношението на детерминантите. Знаменателят съдържа детерминантата на системата, а числителят съдържа детерминантата, получена от детерминантата на системата чрез заместване на коефициентите на това неизвестно със свободни членове. Тази теорема е валидна за система от линейни уравнения от произволен ред.

Пример 1.Решете система от линейни уравнения:

Според Теорема на Крамърние имаме:

И така, решението на система (2):

Три случая при решаване на системи от линейни уравнения

Както става ясно от Теорема на Крамър, при решаване на система от линейни уравнения могат да възникнат три случая:

Първи случай: система от линейни уравнения има уникално решение

(системата е последователна и категорична)

*

Втори случай: система от линейни уравнения има безкраен брой решения

(системата е последователна и несигурна)

**
,

тези. коефициентите на неизвестните и свободните членове са пропорционални.

Трети случай: системата от линейни уравнения няма решения

(системата е непоследователна)

Така че системата млинейни уравнения с ннаречени променливи неставни, ако тя няма нито едно решение, и става, ако има поне едно решение. Нарича се едновременна система от уравнения, която има само едно решение определени, и повече от един – несигурен.

Примери за решаване на системи от линейни уравнения по метода на Крамер

Нека се даде системата

.

Въз основа на теоремата на Крамър

………….
,

Където
—

системна детерминанта. Получаваме останалите детерминанти, като заменяме колоната с коефициентите на съответната променлива (неизвестна) със свободни условия:

Пример 2.

.

Следователно системата е категорична. За да намерим решението му, изчисляваме детерминантите

Използвайки формулите на Cramer намираме:

И така, (1; 0; -1) е единственото решение на системата.

За да проверите решенията на системите от уравнения 3 X 3 и 4 X 4, можете да използвате онлайн калкулатор, като използвате метода за решаване на Cramer.

Ако в система от линейни уравнения няма променливи в едно или повече уравнения, то в детерминантата съответните елементи са равни на нула! Това е следващият пример.

Пример 3.Решете система от линейни уравнения по метода на Крамер:

.

Решение. Намираме детерминантата на системата:

Разгледайте внимателно системата от уравнения и детерминантата на системата и повторете отговора на въпроса в кои случаи един или повече елементи от детерминантата са равни на нула. И така, детерминантата не е равна на нула, следователно системата е определена. За да намерим решението му, изчисляваме детерминантите за неизвестните

Използвайки формулите на Cramer намираме:

И така, решението на системата е (2; -1; 1).

За да проверите решенията на системите от уравнения 3 X 3 и 4 X 4, можете да използвате онлайн калкулатор, като използвате метода за решаване на Cramer.

Най-горе на страницата

Направете теста върху Системи от линейни уравнения

Както вече споменахме, ако детерминантата на системата е равна на нула, а детерминантите на неизвестните не са равни на нула, системата е непоследователна, тоест няма решения. Нека илюстрираме със следния пример.

Пример 4.Решете система от линейни уравнения по метода на Крамер:

Решение. Намираме детерминантата на системата:

Детерминантата на системата е равна на нула, следователно системата от линейни уравнения е или непоследователна и определена, или непоследователна, т.е. няма решения. За да изясним, ние изчисляваме детерминанти за неизвестни

Детерминантите на неизвестните не са равни на нула, следователно системата е непоследователна, тоест няма решения.

За да проверите решенията на системите от уравнения 3 X 3 и 4 X 4, можете да използвате онлайн калкулатор, като използвате метода за решаване на Cramer.

При задачи, включващи системи от линейни уравнения, има и такива, в които освен букви, обозначаващи променливи, има и други букви. Тези букви представляват число, най-често реално. На практика такива уравнения и системи от уравнения се дължат на проблеми за търсене на общи свойства на всякакви явления или обекти. Тоест вие сте изобретили някакъв нов материал или устройство и за да опишете свойствата му, които са общи, независимо от размера или количеството на образеца, трябва да решите система от линейни уравнения, където вместо някои коефициенти за променливи има писма. Не е нужно да търсите далеч за примери.

Следващият пример е за подобен проблем, само че броят на уравненията, променливите и буквите, обозначаващи определено реално число, се увеличава.

Пример 6.Решете система от линейни уравнения по метода на Крамер:

Решение. Намираме детерминантата на системата:

Намиране на детерминанти за неизвестни

Използвайки формулите на Cramer намираме:

,

,

.

И накрая, система от четири уравнения с четири неизвестни.

Пример 7.Решете система от линейни уравнения по метода на Крамер:

.

внимание! Методите за изчисляване на детерминанти от четвърти ред няма да бъдат обяснявани тук. За целта отидете в съответния раздел на сайта. Но ще има малки коментари. Решение. Намираме детерминантата на системата:

Малък коментар. В оригиналния детерминант елементите от четвъртия ред бяха извадени от елементите от втория ред, елементите от четвъртия ред, умножени по 2, от елементите от третия ред и елементите от първия ред, умножени по 2, от елементите на четвъртия ред Трансформациите на началните детерминанти с първите три неизвестни се извършват по същата схема. Намиране на детерминанти за неизвестни

За да се преобразува детерминантата за четвъртото неизвестно, елементите на четвъртия ред бяха извадени от елементите на първия ред.

Използвайки формулите на Cramer намираме:

И така, решението на системата е (1; 1; -1; -1).

За да проверите решенията на системите от уравнения 3 X 3 и 4 X 4, можете да използвате онлайн калкулатор, като използвате метода за решаване на Cramer.

Най-внимателните хора вероятно са забелязали, че статията не съдържа примери за решаване на неопределени системи от линейни уравнения. И всичко това, защото е невъзможно да се решат такива системи с помощта на метода на Крамер; може само да се каже, че системата е несигурна. Решенията на такива системи се предоставят по метода на Гаус.

Нямате време да се задълбочите в решението? Можете да поръчате работа!

Най-горе на страницата

Направете теста върху Системи от линейни уравнения

Друго по темата „Системи уравнения и неравенства“

Калкулатор - решаване на системи от уравнения онлайн

Софтуерна реализация на метода на Cramer в C++

Решаване на системи от линейни уравнения чрез метода на заместване и метода на събиране

Решаване на системи от линейни уравнения по метода на Гаус

Условие за съвместимост на система от линейни уравнения.

Теорема на Кронекер-Капели

Решаване на системи от линейни уравнения по матричен метод (обратна матрица)

Системи от линейни неравенства и изпъкнали множества от точки

Начало на темата "Линейна алгебра"

Детерминанти

В тази статия ще се запознаем с едно много важно понятие от клона на линейната алгебра, което се нарича детерминанта.

Бих искал незабавно да отбележа важен момент: понятието детерминанта е валидно само за квадратни матрици (брой редове = брой колони), други матрици го нямат.

Детерминанта на квадратна матрица(детерминант) - числена характеристика на матрицата.

Обозначение на детерминанти: |A|, det A, ∆ А.

Определящо"n" ред е алгебричната сума на всички възможни произведения на неговите елементи, които отговарят на следните изисквания:

1) Всеки такъв продукт съдържа точно „n“ елемента (т.е. детерминанта от 2-ри ред - 2 елемента).

2) Във всеки продукт има представител на всеки ред и всяка колона като фактор.

3) Всеки два фактора във всеки продукт не могат да принадлежат към един и същи ред или колона.

Знакът на продукта се определя от реда на редуване на номерата на колоните, ако елементите в продукта са подредени във възходящ ред на номерата на редовете.

Нека разгледаме няколко примера за намиране на детерминанта на матрица:

За матрица от първи ред (т.е.

Линейни уравнения. Решаване на системи от линейни уравнения. Методът на Крамер.

има само 1 елемент), детерминантата е равна на този елемент:

2. Разгледайте квадратна матрица от втори ред:

3. Помислете за квадратна матрица от трети ред (3×3):

4. Сега нека да разгледаме примери с реални числа:

Правило на триъгълника.

Правилото на триъгълника е начин за изчисляване на детерминантата на матрица, което включва намирането й по следната схема:

Както вече разбирате, методът е наречен правило на триъгълника поради факта, че умножените елементи на матрицата образуват своеобразни триъгълници.

За да разберем това по-добре, нека да разгледаме един пример:

Сега нека разгледаме изчисляването на детерминантата на матрица с реални числа, използвайки правилото на триъгълника:

За да консолидираме материала, който покрихме, нека решим друг практически пример:

Свойства на детерминантите:

1. Ако елементите на ред или колона са равни на нула, то детерминантата е равна на нула.

2. Детерминантата ще промени знака си, ако 2 реда или колони бъдат разменени. Нека да разгледаме това с малък пример:

3. Детерминантата на транспонираната матрица е равна на детерминантата на оригиналната матрица.

4. Детерминантата е равна на нула, ако елементите на един ред са равни на съответните елементи на друг ред (и за колоните). Най-простият пример за това свойство на детерминантите е:

5. Детерминантата е равна на нула, ако нейните 2 реда са пропорционални (също и за колоните). Пример (редове 1 и 2 са пропорционални):

6. Общият множител на ред (колона) може да бъде изваден от определителния знак.

7) Детерминантата няма да се промени, ако съответните елементи на друг ред (колона) се добавят към елементите на всеки ред (колона), умножени по същата стойност. Нека да разгледаме това с пример:

Преглеждания: 57258

Детерминантата (известна още като детерминанта) се намира само в квадратни матрици. Детерминантата не е нищо повече от стойност, съчетаваща всички елементи на матрицата, която се запазва при транспониране на редове или колони. Може да се обозначи като det(A), |A|, Δ(A), Δ, където A може да бъде или матрица, или буква, която я обозначава. Можете да го намерите с помощта на различни методи:

Всички предложени по-горе методи ще бъдат анализирани върху матрици с размер три и по-висок. Детерминантата на двумерна матрица се намира с помощта на три елементарни математически операции, така че намирането на детерминантата на двумерна матрица няма да попадне в нито един от методите. Е, освен като допълнение, но повече за това по-късно.

Нека намерим детерминантата на матрица 2x2:

За да намерим детерминантата на нашата матрица, трябва да извадим произведението на числата на единия диагонал от другия, а именно, т.е.

Примери за намиране на детерминанта на матрици от втори ред

Декомпозиция на ред/колона

Изберете всеки ред или колона в матрицата. Всяко число в избрания ред се умножава по (-1) i+j, където (i,j е номерът на реда, колоната на това число) и се умножава с детерминанта от втори ред, съставена от останалите елементи след задраскване i - ред и j - колона. Нека го анализираме върху матрицата

1. Изберете ред/колона

Например, нека вземем втория ред.

Забележка: Ако не е изрично посочено кой ред да се използва за намиране на детерминантата, изберете реда, който има нула. Ще има по-малко изчисления.

1. Нека направим израз

Не е трудно да се определи, че знакът на числото се променя всеки път. Следователно вместо единици можете да използвате следната таблица:

1. Нека сменим знака на нашите числа

1. Нека намерим детерминантите на нашите матрици

1. Нека преброим всичко

Решението може да се напише така:

Примери за намиране на детерминанта чрез разширяване на ред/колона:

Метод на редукция до триъгълна форма (използвайки елементарни трансформации)

Детерминантата се намира чрез редуциране на матрицата до триъгълна (стъпкова) форма и умножаване на елементите по главния диагонал

Триъгълна матрица е матрица, чиито елементи от едната страна на диагонала са равни на нула.

Когато конструирате матрица, трябва да запомните три прости правила:

1. Всеки път, когато редовете се сменят, детерминантата променя знака на противоположния.
2. Когато умножавате/разделяте един низ с ненулево число, той трябва да бъде разделен (ако е умножен)/умножен (ако е разделен) по него или да изпълни това действие с получената детерминанта.
3. При добавяне на един низ, умножен по число, към друг низ, детерминантата не се променя (умноженият низ приема първоначалната си стойност).

Нека се опитаме да получим нули в първата колона, след това във втората.

Нека да разгледаме нашата матрица:

такаооо За да направя изчисленията по-приятни, бих искал най-близкото число да е отгоре. Можеш да го оставиш, но недей. Добре, имаме двойка на втория ред и четворка на първия.

Нека разменим тези два реда.

Разменихме редовете, сега трябва или да сменим знака на един ред, или накрая да сменим знака на определителя.

Детерминанти. Изчисляване на детерминанти (страница 2)

Ще направим това по-късно.

Сега, за да получите нула в първия ред, умножете първия ред по 2.

Нека извадим първия ред от втория.

Според нашето 3-то правило ние връщаме оригиналния низ в първоначалната му позиция.

Сега нека направим нула в 3-тия ред. Можем да умножим първия ред по 1,5 и да извадим от третия, но работата с дроби носи малко удоволствие. Затова нека намерим число, до което могат да се сведат двата реда - това е 6.

Умножете 3-тия ред по 2.

Сега нека умножим първия ред по 3 и да извадим от 3-тия.

Нека върнем нашия 1-ви ред.

Не забравяйте, че умножихме третия ред по 2, така че след това ще разделим детерминантата на 2.

Има една колона. Сега, за да получим нули във втория - забравете за 1-ви ред - работим с 2-ри ред. Умножете втория ред по -3 и го добавете към третия.

Не забравяйте да върнете втория ред.

Така че изградихме триъгълна матрица. Какво ни остава? Остава само да умножим числата по главния диагонал, което и ще направим.

Е, остава да запомним, че трябва да разделим нашата детерминанта на 2 и да сменим знака.

Правилото на Сарус (Правилото на триъгълниците)

Правилото на Сарус се прилага само за квадратни матрици от трети ред.

Детерминантата се изчислява чрез добавяне на първите две колони отдясно на матрицата, умножаване на елементите на диагоналите на матрицата и тяхното събиране, и изваждане на сбора от противоположните диагонали. Извадете лилавите от оранжевите диагонали.

Правилото на триъгълниците е същото, само картината е различна.

Теорема на Лаплас вижте Разлагане на ред/колона

1.1. Системи от две линейни уравнения и детерминанти от втори ред

Да разгледаме система от две линейни уравнения с две неизвестни:

Коефициенти с неизвестни И имат два индекса: първият показва номера на уравнението, вторият – номера на променливата.

Правилото на Крамър: Решението на системата се намира чрез разделяне на спомагателните детерминанти на основната детерминанта на системата

,

Бележка 1.Използването на правилото на Крамър е възможно, ако детерминантата на системата не е равно на нула.

Бележка 2.Формулите на Крамър са обобщени за системи от по-висок ред.

Пример 1.Решете системата:
.

Решение.

;
;

;

Преглед:

Заключение:Системата е решена правилно:
.

1.2. Системи от три линейни уравнения и детерминанти от трети ред

Да разгледаме система от три линейни уравнения с три неизвестни:

Извиква се детерминанта, съставена от коефициенти за неизвестни системна детерминанта или основна детерминанта:

.

Ако
тогава системата има уникално решение, което се определя от формулите на Крамер:

къде са детерминантите
– се наричат ​​спомагателни и се получават от определителя чрез замяна на неговата първа, втора или трета колона с колона от свободни членове на системата.

Пример 2.Решете системата
.

Нека формираме основните и спомагателни детерминанти:

Остава да разгледаме правилата за изчисляване на детерминанти от трети ред. Има три от тях: правилото за добавяне на колони, правилото на Sarrus, правилото за разлагане.

а) Правилото за добавяне на първите две колони към основната детерминанта:

Изчислението се извършва по следния начин: продуктите на елементите на главния диагонал и паралелите към него вървят с техния знак; с противоположния знак се вземат продуктите на елементите на вторичния диагонал и паралелите към него.

б) Правилото на Сарус:

Със своя знак те вземат произведенията на елементите на главния диагонал и по успоредниците на него, а липсващият трети елемент се взема от срещуположния ъгъл. С противоположния знак се вземат продуктите на елементите на вторичния диагонал и по паралелите към него се взема третият елемент от срещуположния ъгъл.

в) Правило за разлагане по елементи на ред или колона:

Ако
, Тогава .

Алгебрично допълнениее детерминанта от по-нисък ред, получена чрез задраскване на съответния ред и колона и като се вземе предвид знакът
, Където – номер на ред, – номер на колона.

Например,

,
,
и т.н.

Използвайки това правило, изчисляваме спомагателните детерминанти И , като ги разгънете според елементите на първия ред.

След като изчислихме всички детерминанти, намираме променливите, използвайки правилото на Крамър:

Преглед:

Заключение:системата е решена правилно: .

Основни свойства на детерминантите

Трябва да се помни, че детерминантата е номер, намерени по някои правила. Неговото изчисляване може да бъде опростено, ако използваме основни свойства, които са валидни за детерминанти от всякакъв ред.

Имот 1. Стойността на детерминантата няма да се промени, ако всички негови редове се заменят със съответстващи по брой колони и обратно.

Операцията за заместване на редове с колони се нарича транспониране. От това свойство следва, че всяко твърдение, което е вярно за редовете на детерминантата, ще бъде вярно и за неговите колони.

Имот 2. Ако два реда (колони) в детерминантата се разменят, знакът на детерминантата ще се промени на противоположния.

Имот 3. Ако всички елементи на който и да е ред от детерминанта са равни на 0, то детерминантата е равна на 0.

Имот 4. Ако елементите на детерминантния низ се умножат (разделят) по някакво число , тогава стойността на детерминантата ще нараства (намалява) в веднъж.

Ако елементите на един ред имат общ множител, то той може да бъде изваден от детерминантния знак.

Имот 5. Ако детерминантата има два еднакви или пропорционални реда, тогава такава детерминанта е равна на 0.

Имот 6. Ако елементите на който и да е ред от детерминанта са сбор от два члена, тогава детерминантата е равна на сумата от двете детерминанти.

Имот 7. Стойността на детерминантата няма да се промени, ако елементите на един ред се добавят към елементите на друг ред, умножени по същото число.

В този детерминант първо третият ред беше добавен към втория ред, умножен по 2, след това вторият беше изваден от третата колона, след което вторият ред беше добавен към първия и третия, в резултат на което получихме много нули и опростиха изчислението.

Елементарнотрансформации детерминантата се нарича нейното опростяване чрез използването на посочените свойства.

Пример 1.Изчислителна детерминанта

Директното изчисление според едно от правилата, обсъдени по-горе, води до тромави изчисления. Ето защо е препоръчително да използвате свойствата:

а) от ред 1 извадете втория, умножен по 2;

б) от ред II извадете третия, умножен по 3.

В резултат получаваме:

Нека разширим този детерминант в елементите на първата колона, която съдържа само един ненулев елемент.

.

Системи и детерминанти от по-висок порядък

система линейни уравнения с неизвестните могат да бъдат записани по следния начин:

За този случай също е възможно да се съставят главните и спомагателните детерминанти и да се определят неизвестните с помощта на правилото на Крамер. Проблемът е, че детерминанти от по-висок ред могат да бъдат изчислени само чрез понижаване на реда и намаляването им до детерминанти от трети ред. Това може да стане чрез директно разлагане на елементи от редове или колони, както и чрез използване на предварителни елементарни трансформации и по-нататъшно разлагане.

Пример 4.Изчислете детерминанта от четвърти ред

Решениеможем да го намерим по два начина:

а) чрез директно разширяване в елементите на първия ред:

б) чрез предварителни трансформации и по-нататъшно разлагане

Пример 5.Изчислете детерминанта от пети ред, като получите нули в третия ред, като използвате четвъртата колона

извадете третата от втората колона:

извадете третия от втория ред:

Пример 6.Решете системата:

Решение.Нека съставим детерминанта на системата и, като използваме свойствата на детерминантите, я изчислим:

(от първия ред изваждаме третия, а след това в получения детерминант от трети ред от третата колона изваждаме първия, умножен по 2). Определящо
, следователно, формулите на Cramer са приложими.

Нека изчислим останалите детерминанти:

Четвъртата колона беше умножена по 2 и извадена от останалата част

Четвъртата колона беше извадена от първата и след това, умножена по 2, извадена от втората и третата колона.

.

Тук извършихме същите трансформации като за
.

.

Когато намерите първата колона беше умножена по 2 и извадена от останалите.

Според правилото на Крамър имаме:

След като заместим намерените стойности в уравненията, ние сме убедени, че решението на системата е правилно.

2. МАТРИЦИ И ТЯХНОТО ИЗПОЛЗВАНЕ

ПРИ РЕШАВАНЕ НА СИСТЕМИ ОТ ЛИНЕЙНИ УРАВНЕНИЯ

Система от m линейни уравнения с n неизвестнинаречена система на формата

Където a ijИ b i (аз=1,…,м; b=1,…,н) са някои известни числа и x 1 ,…,x n– неизвестен. При обозначаването на коеф a ijпърви индекс азобозначава номера на уравнението, а второто й– числото на неизвестното, на което стои този коефициент.

Коефициентите за неизвестните ще запишем под формата на матрица , което ще извикаме матрица на системата.

Числата от дясната страна на уравненията са b 1 ,…,b mса наречени безплатни членове.

Тоталност нчисла c 1 ,…,c nНаречен решениена дадена система, ако всяко уравнение на системата стане равенство след заместване на числа в него c 1 ,…,c nвместо съответните неизвестни x 1 ,…,x n.

Нашата задача ще бъде да намерим решения на системата. В този случай могат да възникнат три ситуации:

Нарича се система от линейни уравнения, която има поне едно решение става. В противен случай, т.е. ако системата няма решения, тогава тя се извиква неставни.

Нека разгледаме начини за намиране на решения на системата.

МАТРИЧЕН МЕТОД ЗА РЕШАВАНЕ НА СИСТЕМИ ОТ ЛИНЕЙНИ УРАВНЕНИЯ

Матриците позволяват накратко да се напише система от линейни уравнения. Нека е дадена система от 3 уравнения с три неизвестни:

Помислете за матрицата на системата и матрици колони от неизвестни и свободни термини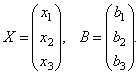

Да намерим работата

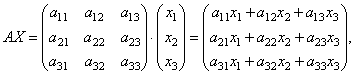
тези. в резултат на произведението получаваме лявата страна на уравненията на тази система. След това, използвайки дефиницията на матрично равенство, тази система може да бъде записана във формата

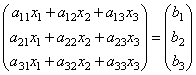или по-кратко А∙X=B.

Ето и матриците АИ бса известни, а матрицата хнеизвестен. Необходимо е да се намери, защото... неговите елементи са решението на тази система. Това уравнение се нарича матрично уравнение.

Нека детерминантата на матрицата е различна от нула | А| ≠ 0. Тогава матричното уравнение се решава по следния начин. Умножете двете страни на уравнението отляво по матрицата А-1, обратна на матрицата А: . Тъй като A -1 A = EИ д∙X = X, тогава получаваме решение на матричното уравнение във формата X = A -1 B .

Имайте предвид, че тъй като обратната матрица може да бъде намерена само за квадратни матрици, матричният метод може да реши само онези системи, в които броят на уравненията съвпада с броя на неизвестните. Въпреки това, матрично записване на системата е възможно и в случай, че броят на уравненията не е равен на броя на неизвестните, тогава матрицата Аняма да бъде квадрат и следователно е невъзможно да се намери решение на системата във формата X = A -1 B.

Примери.Решаване на системи от уравнения.

ПРАВИЛОТО НА КРЕЙМЪР

Да разгледаме система от 3 линейни уравнения с три неизвестни:

Детерминант от трети ред, съответстващ на системната матрица, т.е. съставен от коефициенти за неизвестни,

Наречен детерминанта на системата.

Нека съставим още три детерминанти, както следва: заместваме последователно 1, 2 и 3 колони в детерминанта D с колона от свободни членове

Тогава можем да докажем следния резултат.

Теорема (правило на Крамер).Ако детерминантата на системата Δ ≠ 0, тогава разглежданата система има едно и само едно решение и

Доказателство. И така, нека разгледаме система от 3 уравнения с три неизвестни. Нека умножим първото уравнение на системата по алгебричното допълнение А 11елемент а 11, 2-ро уравнение – на А 21и 3-то – на А 31:

Нека добавим тези уравнения:

Нека разгледаме всяка от скобите и дясната страна на това уравнение. По теоремата за разлагането на детерминантата в елементи от 1-ва колона

По същия начин може да се покаже, че и .

И накрая, това е лесно да се забележи

Така получаваме равенството: .

Следователно, .

Равенствата и се извеждат аналогично, от което следва твърдението на теоремата.

По този начин отбелязваме, че ако детерминантата на системата Δ ≠ 0, тогава системата има уникално решение и обратно. Ако детерминантата на системата е равна на нула, то системата или има безкраен брой решения, или няма решения, т.е. несъвместими.

Примери.Решете система от уравнения

МЕТОД НА ГАУС

Разгледаните по-горе методи могат да се използват за решаване само на онези системи, в които броят на уравненията съвпада с броя на неизвестните и детерминантата на системата трябва да е различна от нула. Методът на Гаус е по-универсален и подходящ за системи с произволен брой уравнения. Състои се в последователно елиминиране на неизвестни от уравненията на системата.

Разгледайте отново система от три уравнения с три неизвестни:

.

Първото уравнение ще оставим непроменено, а от 2-ро и 3-то ще изключим членовете, съдържащи х 1. За да направите това, разделете второто уравнение на А 21 и умножете по – А 11 и след това го добавете към първото уравнение. По същия начин разделяме третото уравнение на А 31 и умножете по – А 11 и след това го съберете с първия. В резултат на това оригиналната система ще приеме формата:

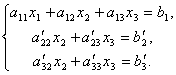
Сега от последното уравнение елиминираме члена, съдържащ х 2. За да направите това, разделете третото уравнение на, умножете по и добавете с второто. Тогава ще имаме система от уравнения:

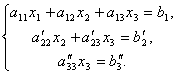
От тук, от последното уравнение е лесно да се намери х 3, след това от 2-ро уравнение х 2и накрая, от 1-ви - х 1.

Когато се използва методът на Гаус, уравненията могат да се разменят, ако е необходимо.

Често, вместо да напишат нова система от уравнения, те се ограничават до написването на разширената матрица на системата:

и след това го приведете в триъгълна или диагонална форма с помощта на елементарни трансформации.

ДА СЕ елементарни трансформацииматриците включват следните трансформации:

1. пренареждане на редове или колони;
2. умножаване на низ по число, различно от нула;
3. добавяне на други редове към един ред.

Примери:Решаване на системи от уравнения по метода на Гаус.

Така системата има безкраен брой решения.

Една система се нарича хомогенна, ако всички свободни членове в нея са равни на нула. Ако такава хомогенна система има характерни детерминанти, тогава последната им колона се състои от нули и всички те са равни на нула. Съвсем очевидно е, че всяка хомогенна система има решение

която отсега нататък ще наричаме нула.

За една хомогенна система основният въпрос е дали тя има решения, различни от нула, и ако има, каква ще бъде съвкупността от всички такива решения. Нека първо разгледаме случая, когато броят на уравненията е равен на броя на неизвестните. Системата ще изглежда така:

Ако детерминантата на тази система е различна от нула, тогава, съгласно теоремата на Крамър, тази система има едно определено решение, а именно в този случай нулевото решение. Ако тази детерминанта е равна на нула, тогава рангът k на таблицата с коефициенти ще бъде по-малък от броя на неизвестните и следователно стойностите на (n - k) неизвестни ще останат напълно произволни и ще имаме безкрайно брой решения, различни от нула. Така стигаме до следната основна теорема:

Теорема I. За да има система (14) решение, различно от нула, е необходимо и достатъчно нейният детерминант да е равен на нула.

Нека сравним резултатите, които получихме за нехомогенната система (1) и хомогенната система (14). Ако детерминантата на системата е различна от нула, то нехомогенната система (1) има едно определено решение, а хомогенната система има само нулево решение. Ако детерминантата на системата е равна на нула, то хомогенната система (14) има решения, различни от нула, но при това условие нееднородната система (1), най-общо казано, изобщо няма решение, тъй като за да за да има решение, е необходимо свободните му членове да са избрани така, че да заличат всички характерни детерминанти. Горният паралелизъм на резултатите ще играе важна роля в бъдеще. По въпросите на физиката хомогенни системи ще се срещат при разглеждане на собствени трептения, а нехомогенни системи - при разглеждане на принудителни колебания, а горният случай на детерминанта, равна на нула, ще характеризира наличието на собствени трептения за хомогенна система и явлението на резонанс за нехомогенна система.

Нека сега преминем към по-подробно разглеждане на решенията на система (14), когато нейният основен детерминант е равен на нула. Нека k е рангът на таблицата на нейните коефициенти и, очевидно, . Съгласно теоремата, доказана в предишния брой, трябва да вземем тези k уравнения, които съдържат основната детерминанта, и да ги решим по отношение на k неизвестни.

Нека приемем, без загуба на общност, че тези неизвестни ще бъдат . Решенията ще бъдат във формата:

където определени числени коефициенти и могат да приемат произволни стойности.

Нека отбележим едно общо свойство на решението на системата (14), което пряко следва от линейността и хомогенността на тази система и което може да се нарече принцип на суперпозиция на решенията, а именно, ако имаме няколко решения на системата:

след това, като ги умножим по произволни константи и ги добавим, също получаваме решение на системата

Процедирайки подобно на това, което направихме за линейни диференциални уравнения, ние наричаме решения (16) линейно независими, ако няма стойности на константите Q, сред които има ненулеви стойности, така че за всяко s са валидни равенствата:

Не е трудно да се конструират линейно независими решения на системата, така че, умножавайки ги по произволни константи и добавяйки ги, да получим всички решения на системата. Наистина, нека се обърнем към формули (15), които дават общото решение на системата и въз основа на тези формули конструираме решения, както следва: в първото решение поставяме a и всички останали равни на нула; във второто решение задаваме a и всички останали равни на нула и т.н. и накрая, в последното решение задаваме всички останали равни на нула. Лесно се вижда, че построените решения са линейно независими, тъй като всяко от тях съдържа едно от неизвестните, равно на единица, което в останалите решения е равно на нула. Нека означим получените решения по следния начин.