Harmonic equation. Fluctuations. Harmonic vibrations. Oscillation characteristics: amplitude, period, frequency, cyclic frequency, phase

Harmonic oscillation is a phenomenon of periodic change of some quantity, in which the dependence on the argument has the character of a sine or cosine function. For example, a quantity that varies in time as follows harmonically fluctuates:

where x is the value of the changing quantity, t is time, the remaining parameters are constant: A is the amplitude of the oscillations, ω is the cyclic frequency of the oscillations, is the full phase of the oscillations, is the initial phase of the oscillations.

Generalized harmonic oscillation in differential form

(Any non-trivial solution of this differential equation is a harmonic oscillation with a cyclic frequency)

Types of vibrations

Free oscillations are performed under the action of the internal forces of the system after the system has been taken out of equilibrium. For free oscillations to be harmonic, it is necessary that the oscillatory system be linear (described by linear equations of motion), and there should be no energy dissipation in it (the latter would cause damping).

Forced oscillations are performed under the influence of an external periodic force. For them to be harmonic, it is sufficient that the oscillatory system be linear (described by linear equations of motion), and the external force itself changes over time as a harmonic oscillation (that is, that the time dependence of this force is sinusoidal).

Harmonic vibration equation

Equation (1)

gives the dependence of the fluctuating value S on time t; this is the equation of free harmonic oscillations in explicit form. However, the equation of oscillations is usually understood as a different record of this equation, in differential form. For definiteness, we take equation (1) in the form

Differentiate it twice with respect to time:

It can be seen that the following relation holds:

which is called the equation of free harmonic oscillations (in differential form). Equation (1) is a solution to differential equation (2). Since equation (2) is a second-order differential equation, two initial conditions are necessary to obtain a complete solution (that is, to determine the constants A and   included in equation (1); for example, the position and speed of an oscillatory system at t = 0.

A mathematical pendulum is an oscillator, which is a mechanical system consisting of a material point located on a weightless inextensible thread or on a weightless rod in a uniform field of gravitational forces. The period of small eigenoscillations of a mathematical pendulum of length l, motionlessly suspended in a uniform gravitational field with free fall acceleration g, is equal to

and does not depend on the amplitude and mass of the pendulum.

A physical pendulum is an oscillator, which is a rigid body that oscillates in the field of any forces about a point that is not the center of mass of this body, or a fixed axis perpendicular to the direction of the forces and not passing through the center of mass of this body.

The simplest type of vibrations are harmonic vibrations- fluctuations in which the displacement of the oscillating point from the equilibrium position changes over time according to the sine or cosine law.

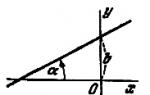
So, with a uniform rotation of the ball around the circumference, its projection (shadow in parallel rays of light) makes a harmonic oscillatory motion on a vertical screen (Fig. 13.2).

The displacement from the equilibrium position during harmonic vibrations is described by an equation (it is called the kinematic law of harmonic motion) of the form:

\(x = A \cos \Bigr(\frac(2 \pi)(T)t + \varphi_0 \Bigl)\) or \(x = A \sin \Bigr(\frac(2 \pi)(T) t + \varphi"_0 \Bigl)\)

where X- mixing - a value that characterizes the position of the oscillating point at the moment of time t relative to the equilibrium position and measured by the distance from the equilibrium position to the position of the point at a given point in time; BUT- oscillation amplitude - the maximum displacement of the body from the equilibrium position; T- oscillation period - the time of one complete oscillation; those. the smallest period of time after which the values of physical quantities characterizing the oscillation are repeated; \(\varphi_0\) - initial phase; \(\varphi = \frac(2 \pi)(T)t + \varphi"_0\) - phase of oscillation at time t. The oscillation phase is an argument of a periodic function, which, for a given oscillation amplitude, determines the state of the oscillatory system (displacement, speed, acceleration) of the body at any time.

If at the initial time t0 = 0 the oscillating point is maximally displaced from the equilibrium position, then \(\varphi_0 = 0\), and the displacement of the point from the equilibrium position changes according to the law

\(x = A \cos \frac(2 \pi)(T)t.\)

If the oscillating point at t 0 = 0 is in a position of stable equilibrium, then the displacement of the point from the equilibrium position changes according to the law

\(x = A \sin \frac(2 \pi)(T)t.\)

the value V, the reciprocal of the period and equal to the number of complete oscillations performed in 1 s, is called oscillation frequency:

\(\nu = \frac(1)(T) \)(in SI the unit of frequency is hertz, 1Hz = 1s -1).

If in time t body commits N full swing, then

\(T = \frac(t)(N) ; \nu = \frac(N)(t).\)

The value \(\omega = 2 \pi \nu = \frac(2 \pi)(T)\) , showing how many oscillations the body makes in 2 \(\pi\) With, called cyclic (circular) frequency.

The kinematic law of harmonic motion can be written as:

\(x = A \cos(2\pi \nu t + \varphi_0), x = A \cos(\omega t + \varphi_0).\)

Graphically, the dependence of the displacement of an oscillating point on time is represented by a cosine (or sinusoid).

Figure 13.3, a shows the time dependence of the displacement of the oscillating point from the equilibrium position for the case \(\varphi_0=0\), i.e. \(~x=A\cos \omega t.\)

Let us find out how the speed of an oscillating point changes with time. To do this, we find the time derivative of this expression:

\(\upsilon_x = x" A \sin \omega t = \omega A \cos \Bigr(\omega t + \frac(\pi)(2) \Bigl) ,\)

where \(~\omega A = |\upsilon_x|_m\) is the amplitude of the velocity projection on the axis X.

This formula shows that during harmonic oscillations, the projection of the body's velocity on the x axis also changes according to the harmonic law with the same frequency, with a different amplitude, and is ahead of the mixing phase by \(\frac(\pi)(2)\) (Fig. 13.3 , b).

To find out the dependence of the acceleration a x (t) find the time derivative of the velocity projection:

\(~ a_x = \upsilon_x" = -\omega^2 A \cos \omega t = \omega^2 \cos(\omega t + \pi),\)

where \(~\omega^2 A = |a_x|_m\) is the amplitude of the acceleration projection onto the axle X.

For harmonic vibrations, the projection acceleration ahead of the phase shift by k (Fig. 13.3, c).

Similarly, you can plot \(~x(t), \upsilon_x (t)\) and \(~a_x(t),\) if \(~x = A \sin \omega t\) with \(\varphi_0 =0.\)

Considering that \(A \cos \omega t = x\), the formula for acceleration can be written

\(~a_x = - \omega^2 x,\)

those. for harmonic oscillations, the acceleration projection is directly proportional to the displacement and opposite in sign, i.e. acceleration is directed in the direction opposite to the displacement.

So, the acceleration projection is the second derivative of the displacement and x \u003d x "", then the resulting ratio can be written as:

\(~a_x + \omega^2 x = 0\) or \(~x"" + \omega^2 x = 0.\)

The last equality is called equation of harmonic oscillations.

A physical system in which harmonic oscillations can exist is called harmonic oscillator, and the equation of harmonic oscillations - harmonic oscillator equation.

Literature

Aksenovich L. A. Physics in high school: Theory. Tasks. Tests: Proc. allowance for institutions providing general. environments, education / L. A. Aksenovich, N. N. Rakina, K. S. Farino; Ed. K. S. Farino. - Mn.: Adukatsia i vykhavanne, 2004. - S. 368-370.

Maximum speed and acceleration values

After analyzing the equations of dependence v(t) and a(t), one can guess that the maximum values of speed and acceleration are taken when the trigonometric factor is equal to 1 or -1. Determined by the formula

How to get dependencies v(t) and a(t)

7. Free vibrations. Velocity, acceleration and energy of oscillatory motion. Addition of vibrations

Free vibrations(or natural vibrations) are vibrations of an oscillatory system, performed only due to the initially reported energy (potential or kinetic) in the absence of external influences.

Potential or kinetic energy can be communicated, for example, in mechanical systems through an initial displacement or an initial velocity.

Freely oscillating bodies always interact with other bodies and together with them form a system of bodies called oscillatory system.

For example, a spring, a ball, and a vertical post to which the upper end of the spring is attached (see figure below) are included in an oscillatory system. Here the ball slides freely along the string (friction forces are negligible). If you take the ball to the right and leave it to itself, it will oscillate freely around the equilibrium position (point O) due to the action of the elastic force of the spring directed towards the equilibrium position.

Another classic example of a mechanical oscillatory system is the mathematical pendulum (see figure below). AT this case the ball oscillates freely under the action of two forces: the force of gravity and the elastic force of the thread (the Earth also enters the oscillatory system). Their resultant is directed to the equilibrium position.

The forces acting between the bodies of an oscillatory system are called internal forces. Outside forces called the forces acting on the system from the bodies that are not included in it. From this point of view, free oscillations can be defined as oscillations in a system under the action of internal forces after the system is taken out of equilibrium.

The conditions for the occurrence of free oscillations are:

1) the emergence of a force in them that returns the system to a position of stable equilibrium after it has been taken out of this state;

2) no friction in the system.

Dynamics of free oscillations.

Vibrations of a body under the action of elastic forces. The equation of oscillatory motion of a body under the action of an elastic force F(see Fig.) can be obtained taking into account Newton's second law ( F = ma) and Hooke's law ( F control= -kx), where m is the mass of the ball, and is the acceleration acquired by the ball under the action of the elastic force, k- coefficient of spring stiffness, X- displacement of the body from the equilibrium position (both equations are written in projection onto the horizontal axis Oh). Equating the right sides of these equations and taking into account that the acceleration a is the second derivative of the coordinate X(offsets), we get:

This is a differential equation of motion of a body oscillating under the action of an elastic force: the second derivative of the coordinate with respect to time (the acceleration of the body) is directly proportional to its coordinate, taken with the opposite sign.

Oscillations of a mathematical pendulum. To obtain the equation for the oscillation of a mathematical pendulum (figure), it is necessary to expand the force of gravity F T= mg to normal F n(directed along the thread) and tangential F τ(tangent to the trajectory of the ball - a circle) components. Normal component of gravity F n and the elastic force of the thread Fynp in total they give the pendulum a centripetal acceleration, which does not affect the magnitude of the speed, but only changes its direction, and the tangential component F τ is the force that returns the ball to its equilibrium position and causes it to oscillate. Using, as in the previous case, Newton's law for tangential acceleration ma τ = F τ and given that F τ= -mg sinα, we get:

a τ= -g sinα,

The minus sign appeared because the force and the angle of deviation from the equilibrium position α have opposite signs. For small deflection angles sinα ≈ α. In its turn, α = s/l, where s- arc OA, I- thread length. Given that and τ= s", we finally get:

The form of the equation is similar to the equation . Only here the parameters of the system are the length of the thread and the acceleration of free fall, and not the stiffness of the spring and the mass of the ball; the role of the coordinate is played by the length of the arc (i.e., the path traveled, as in the first case).

Thus, free oscillations are described by equations of the same type (subject to the same laws) regardless of the physical nature of the forces that cause these oscillations.

Solving equations and is a function of the form:

x = xmcos ω 0t(or x = xmsin ω 0t).

That is, the coordinate of a body that performs free oscillations changes over time according to the cosine or sine law, and, therefore, these oscillations are harmonic:

In the equation x = xmcos ω 0t(or x = xmsin ω 0t), x m- oscillation amplitude, ω 0 - own cyclic (circular) oscillation frequency.

The cyclic frequency and the period of free harmonic oscillations are determined by the properties of the system. So, for vibrations of a body attached to a spring, the following relations are true:

The natural frequency is the greater, the greater the stiffness of the spring or the less mass of the load, which is fully confirmed by experience.

For a mathematical pendulum, the following equalities hold:

This formula was first obtained and tested by the Dutch scientist Huygens (a contemporary of Newton).

The period of oscillation increases with the length of the pendulum and does not depend on its mass.

It should be especially noted that harmonic oscillations are strictly periodic (because they obey the sine or cosine law) and even for a mathematical pendulum, which is an idealization of a real (physical) pendulum, they are possible only at small oscillation angles. If the deflection angles are large, the load displacement will not be proportional to the deflection angle (the sine of the angle) and the acceleration will not be proportional to the displacement.

The speed and acceleration of a body that performs free oscillations will also perform harmonic oscillations. Taking the time derivative of the function ( x = xmcos ω 0t(or x = xmsin ω 0t)), we get the expression for the speed:

v = -v msin ω 0t = -v mx mcos (ω 0t + π/2),

where v m= ω 0 x m- velocity amplitude.

Similarly, the expression for acceleration a we get by differentiating ( v = -v msin ω 0t = -v mx mcos (ω 0t + π/2)):

a = -a mcos ω 0t,

where a m= ω 2 0x m- acceleration amplitude. Thus, the amplitude of the speed of harmonic oscillations is proportional to the frequency, and the acceleration amplitude is proportional to the square of the oscillation frequency.

HARMONIC OSCILLATIONS
Fluctuations in which changes in physical quantities occur according to the cosine or sine law (harmonic law), called. harmonic vibrations. For example, in the case of mechanical harmonic vibrations: In these formulas, ω is the oscillation frequency, x m is the oscillation amplitude, φ 0 and φ 0 ’ are the initial phases of the oscillation. The above formulas differ in the definition of the initial phase and at φ 0 ’ = φ 0 + π/2 completely coincide.
This is the simplest form of periodic oscillations. The specific form of the function (sine or cosine) depends on the way the system is brought out of equilibrium. If the withdrawal occurs with a push (kinetic energy is reported), then at t=0 the displacement x=0, therefore, it is more convenient to use the sin function, setting φ 0 '=0; when deviating from the equilibrium position (potential energy is reported) at t=0, the displacement x=x m, therefore, it is more convenient to use the function cos and φ 0 =0.
An expression under the sign cos or sin, called. oscillation phase:. The phase of the oscillation is measured in radians and determines the value of the displacement (fluctuating value) at a given time.
The oscillation amplitude depends only on the initial deviation (the initial energy imparted to the oscillatory system).
Velocity and acceleration in harmonic oscillations.
According to the definition of speed, speed is the derivative of the coordinate with respect to time
Thus, we see that the speed during harmonic oscillatory motion also changes according to the harmonic law, but the speed fluctuations are ahead of the displacement fluctuations in phase by π/2.
The value is the maximum speed of oscillatory motion (amplitude of speed fluctuations).
Therefore, for the speed during harmonic oscillation we have: , and for the case of a zero initial phase (see graph).
According to the definition of acceleration, acceleration is the derivative of speed with respect to time: is the second derivative of the coordinate with respect to time. Then: . Acceleration during harmonic oscillatory motion also changes according to the harmonic law, but acceleration oscillations are ahead of velocity oscillations by π/2 and displacement oscillations by π (they say that oscillations occur out of phase).
Value - maximum acceleration (amplitude of acceleration fluctuations). Therefore, for acceleration we have: , and for the case of zero initial phase: (see graph).
From the analysis of the process of oscillatory motion, graphs and corresponding mathematical expressions, it can be seen that when the oscillating body passes the equilibrium position (displacement is zero), the acceleration is zero, and the speed of the body is maximum (the body passes the equilibrium position by inertia), and when the amplitude value of the displacement is reached, the speed is equal to zero, and the acceleration is maximal in absolute value (the body changes the direction of its motion).
Let us compare the expressions for displacement and acceleration for harmonic oscillations: and .
You can write: - i.e. the second derivative of the displacement is directly proportional (with the opposite sign) to the displacement. Such an equation is called harmonic oscillation equation. This dependence is satisfied for any harmonic oscillation, regardless of its nature. Since we have not used the parameters of a specific oscillatory system anywhere, only the cyclic frequency can depend on them.
It is often convenient to write the equations for oscillations in the form: , where T is the oscillation period. Then, if time is expressed in fractions of a period, the calculations will be simplified. For example, if you need to find the offset after 1/8 of the period, we get: . Similarly for speed and acceleration.

It is not uncommon for a system to simultaneously participate in two or more independent oscillations. In these cases, a complex oscillatory motion is formed, which is created by superimposing (adding) vibrations to each other. Obviously, the cases of summation of oscillations can be very diverse. They depend not only on the number of added oscillations, but also on the oscillation parameters, on their frequencies, phases, amplitudes, directions. It is not possible to review all the possible variety of cases of summation of oscillations, therefore we will confine ourselves to considering only individual examples.
1. Addition of vibrations in one direction. Let us add two oscillations of the same frequency, but different phases and amplitudes.

(4.40)
When the oscillations are superimposed on each other

We introduce new parameters A and j according to the equations:

(4.42)
The system of equations (4.42) is easily solved.

(4.43)

(4.44)
Thus, for x we finally obtain the equation

(4.45)
So, as a result of adding unidirectional oscillations of the same frequency, we obtain a harmonic (sinusoidal) oscillation, the amplitude and phase of which is determined by formulas (4.43) and (4.44).
Let us consider special cases in which the ratios between the phases of two summed oscillations are different:

(4.46)
Let us now add unidirectional oscillations of the same amplitude, the same phases, but different frequencies.

(4.47)
Let us consider the case when the frequencies are close to each other, i.e. w1~w2=w
Then we will approximately assume that (w1+w2)/2= w, and (w2-w1)/2 is small. The resulting oscillation equation will look like:

(4.48)
Its graph is shown in fig. 4.5 This oscillation is called a beat. It is carried out with a frequency w but its amplitude oscillates with a large period.

2. Addition of two mutually perpendicular oscillations. Let us assume that one oscillation is carried out along the x-axis, the other - along the y-axis. The resulting motion is obviously located in the xy plane.
1. Let us assume that the oscillation frequencies and phases are the same, but the amplitudes are different.

(4.49)
To find the trajectory of the resulting motion, it is necessary to exclude time from equations (4.49). To do this, it is enough to divide term by term one equation by another, as a result of which we get

(4.50)
Equation (4.50) shows that in this case, the addition of oscillations leads to oscillation along a straight line, the tangent of the slope angle of which is determined by the ratio of the amplitudes.
2. Let the phases of the added oscillations differ from each other by /2 and the equations have the form:

(4.51)
To find the trajectory of the resulting motion, excluding time, it is necessary to square the equations (4.51), first dividing them by A1 and A2, respectively, and then adding them up. The trajectory equation will take the form:

(4.52)
This is the equation of an ellipse. It can be proved that for any initial phases and any amplitudes of two added mutually perpendicular oscillations of the same frequency, the resulting oscillation will be carried out along an ellipse. Its orientation will depend on the phases and amplitudes of the added oscillations.
If the added oscillations have different frequencies, then the trajectories of the resulting motions are very diverse. Only if the oscillation frequencies in x and y are multiples of each other, closed trajectories are obtained. Such movements can be attributed to the number of periodic ones. In this case, the trajectories of movements are called Lissajous figures. Let's consider one of the Lissajous figures, which is obtained by adding oscillations with frequency ratios of 1:2, with the same amplitudes and phases at the beginning of the movement.

(4.53)
Along the y axis, oscillations occur twice as often as along the x axis. The addition of such oscillations will lead to a motion trajectory in the form of a figure eight (Fig. 4.7).

8. Damped oscillations and their parameters: decrement and oscillation coefficient, relaxation time

)Period of damped oscillations:

T = (58)

At δ << ω o vibrations do not differ from harmonic ones: T = 2π/ o.

2) Amplitude of damped oscillations is expressed by formula (119).

3) damping decrement, equal to the ratio of two successive oscillation amplitudes BUT(t) and BUT(t+T), characterizes the rate of amplitude decrease over the period:

= e d T (59)

4) Logarithmic damping decrement- natural logarithm of the ratio of the amplitudes of two successive oscillations corresponding to time points that differ by a period

q \u003d ln \u003d ln e d T \u003d dT(60)

The logarithmic damping decrement is a constant value for a given oscillatory system.

5) Relaxation time called the period of time ( t) during which the amplitude of damped oscillations decreases by a factor of e:

e d τ = e, δτ = 1,

t = 1/d, (61)

From the comparison of expressions (60) and (61) we obtain:

q= = , (62)

where N e - the number of oscillations made during the relaxation time.

If during the time t the system makes Ν fluctuations, then t = Ν . Τ and the equation of damped oscillations can be represented as:

S \u003d A 0 e -d N T cos(w t+j)\u003d A 0 e -q N cos(w t+j).

6)Quality factor of the oscillatory system(Q) it is customary to call the quantity characterizing the energy loss in the system during the oscillation period:

Q= 2p , (63)

where W is the total energy of the system, ∆W is the energy dissipated over the period. The less energy dissipated, the greater the quality factor of the system. Calculations show that

Q = = pNe = = . (64)

Τᴀᴋᴎᴍ ᴏϬᴩᴀᴈᴏᴍ, the quality factor is inversely proportional to the logarithmic damping decrement. From formula (64) it follows that the quality factor is proportional to the number of oscillations N e performed by the system during the relaxation time.

7) Potential energy system at time t can be expressed in terms of potential energy W 0 at largest deviation:

W = = kA o 2 e -2 qN = W 0 e -2 qN . (65)

It is usually conditionally considered that oscillations have practically ceased if their energy has decreased by a factor of 100 (the amplitude has decreased by a factor of 10). From here you can get an expression for calculating the number of oscillations made by the system:

= e 2qN= 100, ln100 = 2 qN;

N = = . (66)

9. Forced vibrations. Resonance. aperiodic fluctuations. Self-oscillations.

In order for the system to perform undamped oscillations, it is necessary to replenish the energy losses of oscillations due to friction from the outside. To ensure that the energy of the system's oscillations does not decrease, a force is usually introduced that periodically acts on the system (we will call such a force compelling, and forced oscillations).

DEFINITION: forced called such vibrations that occur in an oscillatory system under the action of an external periodically changing force.

This force, as a rule, performs a dual role:

firstly, it shakes the system and gives it a certain amount of energy;

secondly, it periodically replenishes energy losses (energy consumption) to overcome the forces of resistance and friction.

Let the driving force change with time according to the law:

Let us compose an equation of motion for a system oscillating under the influence of such a force. We assume that the system is also affected by the quasi-elastic force and the drag force of the medium (which is valid under the assumption of small oscillations). Then the equation of motion of the system will look like:

Or .

By substituting , , – the natural frequency of the system oscillations, we obtain a non-homogeneous linear differential equation 2 th order:

It is known from the theory of differential equations that the general solution of an inhomogeneous equation is equal to the sum of the general solution of a homogeneous equation and the particular solution of an inhomogeneous equation.

The general solution of the homogeneous equation is known:

where ; a 0 and a– arbitrary const.

Using a vector diagram, you can make sure that such an assumption is true, and also determine the values of “ a" and " j”.

The oscillation amplitude is determined by the following expression:

Meaning " j”, which is the magnitude of the phase delay of the forced oscillation from the driving force that caused it, is also determined from the vector diagram and is:

Finally, a particular solution of the inhomogeneous equation will take the form:

(8.18)

This function, together with

(8.19)

gives a general solution to an inhomogeneous differential equation describing the behavior of a system under forced vibrations. The term (8.19) plays a significant role in the initial stage of the process, during the so-called establishment of oscillations (Fig. 8.10). In the course of time, due to the exponential factor, the role of the second term (8.19) decreases more and more, and after a sufficient time it can be neglected, keeping only the term (8.18) in the solution.

Thus, function (8.18) describes steady forced oscillations. They are harmonic oscillations with a frequency equal to the frequency of the driving force. The amplitude of forced oscillations is proportional to the amplitude of the driving force. For a given oscillatory system (defined w 0 and b) the amplitude depends on the frequency of the driving force. Forced oscillations lag behind the driving force in phase, and the amount of lag "j" also depends on the frequency of the driving force.

The dependence of the amplitude of forced oscillations on the frequency of the driving force leads to the fact that at a certain frequency determined for a given system, the oscillation amplitude reaches its maximum value. The oscillatory system is especially responsive to the action of the driving force at this frequency. This phenomenon is called resonance, and the corresponding frequency is resonant frequency.

DEFINITION: a phenomenon in which a sharp increase in the amplitude of forced oscillations is observed is called resonance.

The resonant frequency is determined from the maximum condition for the amplitude of forced oscillations:

. (8.20)

Then, substituting this value into the expression for the amplitude, we get:

. (8.21)

In the absence of medium resistance, the amplitude of oscillations at resonance would turn to infinity; the resonant frequency under the same conditions (b=0) coincides with the natural oscillation frequency.

The dependence of the amplitude of forced oscillations on the frequency of the driving force (or, what is the same, on the frequency of oscillations) can be represented graphically (Fig. 8.11). Separate curves correspond to different values of “b”. The smaller “b”, the higher and to the right lies the maximum of this curve (see the expression for w res.). With very large damping, resonance is not observed - with increasing frequency, the amplitude of forced oscillations decreases monotonically (lower curve in Fig. 8.11).

The set of presented graphs corresponding to different values of b is called resonance curves.

Remarks about resonance curves:

as w®0 tends, all curves come to the same nonzero value equal to . This value represents the displacement from the equilibrium position that the system receives under the action of a constant force F 0 .

as w®¥ all curves tend asymptotically to zero, since at a high frequency, the force changes its direction so quickly that the system does not have time to noticeably shift from the equilibrium position.

the smaller b, the stronger the amplitude near the resonance changes with frequency, the "sharper" the maximum.

The phenomenon of resonance is often useful, especially in acoustics and radio engineering.

Self-oscillations- undamped oscillations in a dissipative dynamic system with nonlinear feedback, supported by the energy of the constant, that is non-periodic external influence.

Self-oscillations are different from forced vibrations because the latter are caused periodical external influence and occur with the frequency of this influence, while the occurrence of self-oscillations and their frequency are determined by the internal properties of the self-oscillatory system itself.

Term self-oscillations introduced into Russian terminology by A. A. Andronov in 1928.

Examples[

Examples of self-oscillations are:

· undamped oscillations of the clock's pendulum due to the constant action of the gravity of the clockwork weight;

vibrations of a violin string under the influence of a uniformly moving bow

the occurrence of alternating current in the multivibrator circuits and in other electronic generators at a constant supply voltage;

fluctuation of the air column in the pipe of the organ, with a uniform supply of air into it. (see also Standing wave)

rotational oscillations of a brass clock gear with a steel axis suspended from a magnet and twisted (Gamazkov's experiment) (the kinetic energy of the wheel, as in a unipolar generator, is converted into the potential energy of the electric field, the potential energy of the electric field, as in a unipolar engine, is converted into the kinetic energy of the wheel etc.)

Maklakov hammer

A hammer that strikes due to the energy of alternating current with a frequency many times lower than the frequency of the current in the electric circuit.

The coil L of the oscillatory circuit is placed above the table (or other object that needs to be hit). From below, an iron tube enters into it, the lower end of which is the impact part of the hammer. The tube has a vertical slot to reduce the Foucault currents. The parameters of the oscillatory circuit are such that the natural frequency of its oscillations coincides with the frequency of the current in the circuit (for example, alternating city current, 50 hertz).

After the current is turned on and oscillations are established, a resonance of the currents of the circuit and the external circuit is observed, and the iron tube is drawn into the coil. The inductance of the coil increases, the oscillatory circuit goes out of resonance, and the amplitude of the current oscillations in the coil decreases. Therefore, the tube returns to its original position - outside the coil - under the influence of gravity. Then the current fluctuations inside the circuit begin to grow, and resonance sets in again: the tube is again drawn into the coil.

tube commits self-oscillations, that is, periodic movements up and down, and at the same time it knocks loudly on the table, like a hammer. The period of these mechanical self-oscillations is tens of times greater than the period of the alternating current supporting them.

The hammer is named after M. I. Maklakov, a lecture assistant at the Moscow Institute of Physics and Technology, who proposed and carried out such an experiment to demonstrate self-oscillations.

Mechanism of self-oscillations

Fig 1. Mechanism of self-oscillations

Self-oscillations can have a different nature: mechanical, thermal, electromagnetic, chemical. The mechanism of occurrence and maintenance of self-oscillations in different systems can be based on different laws of physics or chemistry. For an accurate quantitative description of self-oscillations of different systems, different mathematical apparatus may be required. Nevertheless, it is possible to imagine a scheme that is common to all self-oscillating systems and qualitatively describes this mechanism (Fig. 1).

On the diagram: S- source of constant (non-periodic) impact; R- a non-linear controller that converts a constant effect into a variable (for example, intermittent in time), which “swings” oscillator V- oscillating element (elements) of the system, and oscillations of the oscillator through feedback B control the operation of the regulator R, setting phase and frequency his actions. Dissipation (dissipation of energy) in a self-oscillatory system is compensated by the energy entering it from a source of constant influence, due to which self-oscillations do not decay.

Rice. 2 Scheme of the ratchet mechanism of a pendulum clock

If an oscillating element of the system is capable of its own damped oscillations(so-called. harmonic dissipative oscillator), self-oscillations (with equal dissipation and energy input into the system during the period) are established at a frequency close to resonant for this oscillator, their shape becomes close to harmonic, and the amplitude, in a certain range of values, the greater, the greater the magnitude of the constant external influence.

An example of such a system is the ratchet mechanism of a pendulum clock, the diagram of which is shown in Fig. 2. On the ratchet wheel axle A(which in this system performs the function of a non-linear controller) there is a constant moment of force M transmitted through the gear from the mainspring or from the weight. When the wheel spins A its teeth impart short-term impulses of force to the pendulum P(oscillator), thanks to which its oscillations do not fade. The kinematics of the mechanism plays the role of feedback in the system, synchronizing the rotation of the wheel with the oscillations of the pendulum in such a way that during the full period of oscillation the wheel turns through an angle corresponding to one tooth.

Self-oscillating systems that do not contain harmonic oscillators are called relaxation. Oscillations in them can be very different from harmonic ones, and have a rectangular, triangular or trapezoidal shape. The amplitude and period of relaxation self-oscillations are determined by the ratio of the magnitude of the constant action and the characteristics of the inertia and dissipation of the system.

Rice. 3 Electric bell

The simplest example of relaxation self-oscillations is the operation of an electric bell, shown in Fig. 3. The source of constant (non-periodic) exposure here is an electric battery U; the role of a non-linear controller is performed by a chopper T, closing and opening the electrical circuit, as a result of which an intermittent current arises in it; oscillating elements are a magnetic field periodically induced in the core of an electromagnet E, and anchor A moving under the influence of an alternating magnetic field. The oscillations of the armature actuate the chopper, which forms the feedback.

The inertia of this system is determined by two different physical quantities: the moment of inertia of the armature BUT and the inductance of the electromagnet winding E. An increase in any of these parameters leads to an increase in the period of self-oscillations.

If there are several elements in the system that oscillate independently of each other and simultaneously act on a nonlinear controller or controllers (of which there may also be several), self-oscillations can take on a more complex character, for example, aperiodic, or dynamic chaos.

In nature and technology

Self-oscillations underlie many natural phenomena:

fluctuations of plant leaves under the action of a uniform air flow;

· formation of turbulent flows on riffles and rapids of rivers;

The action of regular geysers, etc.

The principle of operation of a large number of various technical devices and devices is based on self-oscillations, including:

work of all kinds of clocks, both mechanical and electric;

· sounding of all wind and string-bowed musical instruments;

fluctuations called movements or processes that are characterized by a certain repetition in time. Oscillatory processes are widespread in nature and technology, for example, the swing of a clock pendulum, alternating electric current, etc. When the pendulum oscillates, the coordinate of its center of mass changes; in the case of alternating current, the voltage and current in the circuit fluctuate. The physical nature of oscillations can be different, therefore, mechanical, electromagnetic, etc. oscillations are distinguished. However, various oscillatory processes are described by the same characteristics and the same equations. From this comes the feasibility unified approach to the study of vibrations different physical nature.

The fluctuations are called free, if they are made only under the influence of internal forces acting between the elements of the system, after the system is taken out of equilibrium by external forces and left to itself. Free vibrations always damped oscillations because energy losses are inevitable in real systems. In the idealized case of a system without energy loss, free oscillations (continuing as long as desired) are called own.

The simplest type of free undamped oscillations are harmonic oscillations - fluctuations in which the fluctuating value changes with time according to the sine (cosine) law. Oscillations encountered in nature and technology often have a character close to harmonic.

Harmonic vibrations are described by an equation called the equation of harmonic vibrations:

where BUT- amplitude of fluctuations, the maximum value of the fluctuating value X; - circular (cyclic) frequency of natural oscillations; - the initial phase of the oscillation at a moment of time t= 0; - the phase of the oscillation at the moment of time t. The phase of the oscillation determines the value of the oscillating quantity at a given time. Since the cosine varies from +1 to -1, then X can take values from + A before - BUT.

Time T, for which the system completes one complete oscillation, is called period of oscillation. During T oscillation phase is incremented by 2 π , i.e.

Where . (14.2)

The reciprocal of the oscillation period

i.e., the number of complete oscillations per unit time is called the oscillation frequency. Comparing (14.2) and (14.3) we obtain

The unit of frequency is hertz (Hz): 1 Hz is the frequency at which one complete oscillation takes place in 1 s.

Systems in which free vibrations can occur are called oscillators . What properties must a system have in order for free oscillations to occur in it? The mechanical system must have position of stable equilibrium, upon exiting which appears restoring force towards equilibrium. This position corresponds, as is known, to the minimum of the potential energy of the system. Let us consider several oscillatory systems that satisfy the listed properties.

Oscillations arising under the action of external, periodically changing forces (with a periodic supply of energy from the outside to the oscillatory system)

Energy transformation

Spring pendulum

The cyclic frequency and the oscillation period are, respectively:

A material point attached to a perfectly elastic spring

Ø plot of the potential and kinetic energy of a spring pendulum on the x-coordinate.

Ø qualitative graphs of dependences of kinetic and potential energy on time.

Ø Forced

Ø The frequency of forced oscillations is equal to the frequency of changes in the external force

Ø If Fbc changes according to the sine or cosine law, then the forced oscillations will be harmonic

Ø With self-oscillations, a periodic supply of energy from its own source inside the oscillatory system is necessary

Harmonic oscillations are oscillations in which the oscillating value changes with time according to the law of sine or cosine

the equations of harmonic oscillations (the laws of motion of points) have the form

Harmonic vibrations such oscillations are called, in which the oscillating value varies with time according to the lawsinus orcosine .
Harmonic vibration equation looks like:

,
where A - oscillation amplitude (the value of the greatest deviation of the system from the equilibrium position); -circular (cyclic) frequency. Periodically changing cosine argument - called oscillation phase . The oscillation phase determines the displacement of the oscillating quantity from the equilibrium position at a given time t. The constant φ is the value of the phase at time t = 0 and is called the initial phase of the oscillation . The value of the initial phase is determined by the choice of the reference point. The x value can take values ranging from -A to +A.
The time interval T, after which certain states of the oscillatory system are repeated, called the period of oscillation . Cosine is a periodic function with a period of 2π, therefore, over a period of time T, after which the oscillation phase will receive an increment equal to 2π, the state of the system performing harmonic oscillations will repeat. This period of time T is called the period of harmonic oscillations.
The period of harmonic oscillations is : T = 2π/.
The number of oscillations per unit time is called oscillation frequency ν.
Frequency of harmonic vibrations is equal to: ν = 1/T. Frequency unit hertz(Hz) - one oscillation per second.
Circular frequency = 2π/T = 2πν gives the number of oscillations in 2π seconds.

Generalized harmonic oscillation in differential form

Graphically, harmonic oscillations can be depicted as a dependence of x on t (Fig. 1.1.A), and rotating amplitude method (vector diagram method)(Fig.1.1.B) .

The rotating amplitude method allows you to visualize all the parameters included in the equation of harmonic oscillations. Indeed, if the amplitude vector BUT located at an angle φ to the x-axis (see Figure 1.1. B), then its projection on the x-axis will be equal to: x = Acos(φ). The angle φ is the initial phase. If the vector BUT put into rotation with an angular velocity equal to the circular frequency of oscillations, then the projection of the end of the vector will move along the x-axis and take values ranging from -A to +A, and the coordinate of this projection will change over time according to the law:
.
Thus, the length of the vector is equal to the amplitude of the harmonic oscillation, the direction of the vector at the initial moment forms an angle with the x-axis equal to the initial phase of the oscillation φ, and the change in the direction angle with time is equal to the phase of the harmonic oscillations. The time for which the amplitude vector makes one complete revolution is equal to the period T of harmonic oscillations. The number of revolutions of the vector per second is equal to the oscillation frequency ν.