Given the vertices of a triangle aBC find the equation of the side. Straight line on the plane. Solution examples. What you need to know and be able to successfully solve problems in geometry

How to learn to solve problems in analytical geometry?
Typical problem with a triangle on a plane

This lesson was created on the approach to the equator between the geometry of the plane and the geometry of space. At the moment, there is a need to systematize the accumulated information and answer a very important question: how to learn to solve problems in analytical geometry? The difficulty lies in the fact that there are an infinite number of problems in geometry, and no textbook can contain all the many and variety of examples. Is not function derivative with five rules of differentiation, a table, and a few techniques….

There is a solution! I will not say loud words that I have developed some kind of grandiose technique, however, in my opinion, there is an effective approach to the problem under consideration, which allows even a full kettle to achieve good and excellent results. At least, the general algorithm for solving geometric problems took shape very clearly in my head.

WHAT YOU NEED TO KNOW AND BE ABLE TO
to successfully solve problems in geometry?

There is no getting away from this - in order not to randomly poke buttons with your nose, you need to master the basics of analytical geometry. Therefore, if you have just started studying geometry or have completely forgotten it, please start with the lesson Vectors for dummies. In addition to vectors and actions with them, you need to know the basic concepts of plane geometry, in particular, equation of a straight line in a plane and . The geometry of space is represented by articles Plane equation, Equations of a straight line in space, Basic tasks on a line and a plane and some other lessons. Curved lines and spatial surfaces of the second order stand somewhat apart, and there are not so many specific problems with them.

Suppose a student already has elementary knowledge and skills in solving the simplest problems of analytical geometry. But it happens like this: you read the condition of the problem, and ... you want to close the whole thing altogether, throw it into the far corner and forget it, like a nightmare. Moreover, this does not fundamentally depend on the level of your qualifications, from time to time I myself encounter tasks for which the solution is not obvious. How to act in such cases? No need to be afraid of a task that you do not understand!

Firstly, should be set to is it a "planar" or spatial problem? For example, if vectors with two coordinates appear in the condition, then, of course, this is the geometry of the plane. And if the teacher loaded the grateful listener with a pyramid, then there is clearly the geometry of space. The results of the first step are already quite good, because we managed to cut off a huge amount of information unnecessary for this task!

Second. The condition, as a rule, will concern you with some geometric figure. Indeed, walk along the corridors of your native university, and you will see a lot of anxious faces.

In "flat" problems, not to mention the obvious points and lines, the most popular figure is a triangle. We will analyze it in great detail. Next comes the parallelogram, and the rectangle, square, rhombus, circle, and other figures are much less common.

In spatial tasks, the same flat figures + the planes themselves and common triangular pyramids with parallelepipeds can fly.

Question two - Do you know everything about this figure? Suppose the condition is about an isosceles triangle, and you remember very vaguely what kind of triangle it is. We open a school textbook and read about an isosceles triangle. What to do ... the doctor said a rhombus, so a rhombus. Analytic geometry is analytic geometry, but the problem will help to solve the geometric properties of the figures themselves known to us from the school curriculum. If you do not know what the sum of the angles of a triangle is, then you can suffer for a long time.

Third. ALWAYS try to follow the blueprint(on a draft / clean / mentally), even if this is not required by the condition. In "flat" tasks, Euclid himself ordered to take a ruler with a pencil in hand - and not only in order to understand the condition, but also for the purpose of self-testing. In this case, the most convenient scale is 1 unit = 1 cm (2 tetrad cells). Let's not talk about negligent students and mathematicians spinning in their graves - it is almost impossible to make a mistake in such problems. For spatial tasks, we perform a schematic drawing, which will also help analyze the condition.

A drawing or schematic drawing often immediately allows you to see the way to solve the problem. Of course, for this you need to know the foundation of geometry and cut in the properties of geometric shapes (see the previous paragraph).

fourth. Development of a solution algorithm. Many geometry problems are multi-pass, so it is very convenient to break the solution and its design into points. Often, the algorithm immediately comes to mind after you have read the condition or completed the drawing. In case of difficulties, we start with the QUESTION of the problem. For example, according to the condition "it is required to build a straight line ...". Here the most logical question is: “What is enough to know to build this line?”. Suppose, "we know the point, we need to know the direction vector." We ask the following question: “How to find this direction vector? Where?" etc.

Sometimes there is a "plug" - the task is not solved and that's it. The reasons for the stopper can be the following:

- A serious gap in elementary knowledge. In other words, you do not know or (and) do not see some very simple thing.

- Ignorance of the properties of geometric shapes.

- The task was difficult. Yes, it happens. There is no point in steaming for hours and collecting tears in a handkerchief. Ask your teacher, fellow students or ask a question on the forum for advice. Moreover, it is better to make its statement concrete - about that part of the solution that you do not understand. A cry in the form of "How to solve the problem?" doesn't look good... and above all, for your own reputation.

Stage five. We solve-check, solve-check, solve-check-give an answer. It is beneficial to check each item of the task immediately after it is done. This will help you find the error immediately. Naturally, no one forbids quickly solving the entire problem, but there is a risk of rewriting everything again (often several pages).

Here, perhaps, are all the main considerations that it is advisable to be guided by when solving problems.

The practical part of the lesson is represented by geometry on a plane. There will be only two examples, but it will not seem enough =)

Let's go through the thread of the algorithm that I just reviewed in my little scientific work:

Example 1

Three vertices of a parallelogram are given. Find top.

Let's start to figure it out:

Step one: it is obvious that we are talking about a “flat” problem.

step two: The problem is about a parallelogram. Everyone remembers such a parallelogram figure? No need to smile, a lot of people are educated at 30-40-50 or more years old, so even simple facts can be erased from memory. The definition of a parallelogram is found in Example No. 3 of the lesson Linear (non) dependence of vectors. Vector basis.

Step Three: Let's make a drawing on which we mark three known vertices. It's funny that it's easy to immediately build the desired point:

Constructing is, of course, good, but the solution must be formalized analytically.

Step Four: Development of a solution algorithm. The first thing that comes to mind is that a point can be found as the intersection of lines. Their equations are unknown to us, so we have to deal with this issue:

1) Opposite sides are parallel. By points find the direction vector of these sides . This is the simplest task that was considered in the lesson. Vectors for dummies.

Note: it is more correct to say “the equation of the straight line containing the side”, but hereinafter, for brevity, I will use the phrases “equation of the side”, “directing vector of the side”, etc.

3) Opposite sides are parallel. From the points we find the direction vector of these sides.

4) Compose the equation of a straight line by a point and a direction vector

In paragraphs 1-2 and 3-4, we actually solved the same problem twice, by the way, it is analyzed in example No. 3 of the lesson The simplest problems with a straight line on a plane. It was possible to go a longer way - first find the equations of lines and only then “pull out” the direction vectors from them.

5) Now the equations of the lines are known. It remains to compose and solve the corresponding system of linear equations (see examples No. 4, 5 of the same lesson The simplest problems with a straight line on a plane).

Point found.

The task is quite simple and its solution is obvious, but there is a shorter way!

The second way to solve:

The diagonals of a parallelogram are bisected by their point of intersection. I marked the point, but in order not to clutter up the drawing, I did not draw the diagonals myself.

Compose the equation of the side by points :

To check, mentally or on a draft, substitute the coordinates of each point in the resulting equation. Now let's find the slope. To do this, we rewrite the general equation in the form of an equation with a slope:

So the slope factor is:

Similarly, we find the equations of the sides. I don’t see much point in painting the same thing, so I’ll immediately give the finished result:

2) Find the length of the side. This is the simplest task discussed in the lesson. Vectors for dummies. For points we use the formula:

Using the same formula, it is easy to find the lengths of other sides. Checking is very quickly performed with a regular ruler.

We use the formula .

Let's find the vectors:

In this way:

By the way, along the way, we found the lengths of the sides.

As a result:

Well, it seems to be true, for persuasiveness, you can attach a protractor to the corner.

Attention! Do not confuse the angle of a triangle with the angle between straight lines. The angle of a triangle can be obtuse, but the angle between straight lines is not (see the last paragraph of the article The simplest problems with a straight line on a plane). However, the formulas of the above lesson can also be used to find the angle of a triangle, but the roughness is that those formulas always give an acute angle. With their help, I solved this problem on a draft and got the result. And on the clean copy, you would have to write down additional excuses that.

4) Write the equation of a straight line passing through a point parallel to a straight line.

Standard task, discussed in detail in example No. 2 of the lesson The simplest problems with a straight line on a plane. From the general equation of a straight line pull out the direction vector . Let's compose the equation of a straight line by a point and a directing vector:

How to find the height of a triangle?

5) Let's make the equation of height and we will find its length.

There is no escape from strict definitions, so you have to steal from a school textbook:

triangle height called the perpendicular drawn from the vertex of the triangle to the line containing the opposite side.

That is, it is necessary to compose the equation of the perpendicular drawn from the vertex to the side. This task is considered in examples No. 6, 7 of the lesson The simplest problems with a straight line on a plane. From the equation remove the normal vector. We will compose the height equation for the point and the direction vector:

Please note that we do not know the coordinates of the point.

Sometimes the height equation is found from the ratio of the slopes of the perpendicular lines: . In this case, then: . We will compose the height equation for a point and a slope (see the beginning of the lesson Equation of a straight line on a plane):

The length of the height can be found in two ways.

There is a roundabout way:

a) find - the point of intersection of the height and side;
b) find the length of the segment by two known points.

But in class The simplest problems with a straight line on a plane a convenient formula for the distance from a point to a line was considered. The point is known: , the equation of the line is also known: , In this way:

6) Calculate the area of ​​the triangle. In space, the area of ​​a triangle is traditionally calculated using cross product of vectors, but here a triangle is given in the plane. We use the school formula:
The area of ​​a triangle is half the product of its base times its height.

In this case:

How to find the median of a triangle?

7) Compose the median equation.

Triangle median A line segment joining the vertex of a triangle with the midpoint of the opposite side is called.

a) Find a point - the midpoint of the side. We use midpoint coordinate formulas. The coordinates of the ends of the segment are known: , then the coordinates of the middle:

In this way:

We compose the median equation by points :

To check the equation, you need to substitute the coordinates of the points into it.

8) Find the point of intersection of height and median. I think everyone has already learned how to perform this element of figure skating without falling:

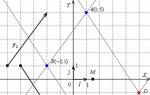
Task 1. The coordinates of the vertices of the triangle ABC are given: A(4; 3), B(16;-6), C(20; 16). Find: 1) the length of the side AB; 2) equations of the sides AB and BC and their slopes; 3) angle B in radians with an accuracy of two decimal places; 4) the equation of height CD and its length; 5) the equation of the median AE and the coordinates of the point K of the intersection of this median with the height CD; 6) the equation of a straight line passing through the point K parallel to the side AB; 7) the coordinates of the point M, located symmetrically to the point A relative to the straight line CD.

Solution:

1. Distance d between points A(x 1 ,y 1) and B(x 2 ,y 2) is determined by the formula

Applying (1), we find the length of the side AB:

2. The equation of a straight line passing through the points A (x 1, y 1) and B (x 2, y 2) has the form

(2)

Substituting in (2) the coordinates of points A and B, we obtain the equation of side AB:

Having solved the last equation for y, we find the equation of the side AB in the form of a straight line equation with a slope:

where

Substituting in (2) the coordinates of points B and C, we obtain the equation of the straight line BC:

Or

3. It is known that the tangent of the angle between two straight lines, the angular coefficients of which are respectively equal and is calculated by the formula

(3)

The desired angle B is formed by the straight lines AB and BC, the angular coefficients of which are found: Applying (3), we obtain

Or glad.

4. The equation of a straight line passing through a given point in a given direction has the form

(4)

The height CD is perpendicular to the side AB. To find the slope of the height CD, we use the condition of perpendicularity of the lines. Since then Substituting into (4) the coordinates of point C and the found angular coefficient of height, we obtain

To find the length of the height CD, we first determine the coordinates of the point D - the point of intersection of the lines AB and CD. Solving the system together:

find those. D(8;0).

Using formula (1), we find the length of the height CD:

5. To find the equation for the median AE, we first determine the coordinates of the point E, which is the midpoint of the side BC, using the formulas for dividing the segment into two equal parts:

(5)

Consequently,

Substituting in (2) the coordinates of points A and E, we find the median equation:

To find the coordinates of the point of intersection of the height CD and the median AE, we jointly solve the system of equations

We find .

6. Since the desired line is parallel to the side AB, then its slope will be equal to the slope of the line AB. Substituting in (4) the coordinates of the found point K and the slope we get

3x + 4y - 49 = 0 (KF)

7. Since the line AB is perpendicular to the line CD, the desired point M, located symmetrically to the point A relative to the line CD, lies on the line AB. In addition, point D is the midpoint of segment AM. Applying formulas (5), we find the coordinates of the desired point M:

Triangle ABC, altitude CD, median AE, line KF and point M are built in the xOy coordinate system in fig. one.

Task 2. Compose an equation for the locus of points, the ratio of the distances of which to a given point A (4; 0) and to a given straight line x \u003d 1 is equal to 2.

Solution:

In the xOy coordinate system, we construct the point A(4;0) and the straight line x = 1. Let M(x;y) be an arbitrary point of the desired locus of points. Let us drop the perpendicular MB to the given line x = 1 and determine the coordinates of the point B. Since the point B lies on the given line, its abscissa is equal to 1. The ordinate of the point B is equal to the ordinate of the point M. Therefore, B(1; y) (Fig. 2 ).

By the condition of the problem |MA|: |MV| = 2. Distances |MA| and |MB| we find by formula (1) of problem 1:

By squaring the left and right sides, we get

or

The resulting equation is a hyperbola, in which the real semi-axis is a = 2, and the imaginary one is

Let us define the foci of the hyperbola. For a hyperbola, the equality is satisfied. Therefore, and are the foci of the hyperbola. As you can see, the given point A(4;0) is the right focus of the hyperbola.

Let us determine the eccentricity of the resulting hyperbola:

The asymptote equations of the hyperbola have the form and . Therefore, or and are asymptotes of the hyperbola. Before constructing a hyperbola, we construct its asymptotes.

Task 3. Compose an equation for the locus of points equidistant from the point A (4; 3) and the straight line y \u003d 1. Reduce the resulting equation to its simplest form.

Solution: Let M(x; y) be one of the points of the desired locus of points. Let us drop the perpendicular MB from the point M to the given line y = 1 (Fig. 3). Let's determine the coordinates of point B. It is obvious that the abscissa of point B is equal to the abscissa of point M, and the ordinate of point B is 1, i.e. B (x; 1). By the condition of the problem |MA|=|MV|. Therefore, for any point M (x; y) belonging to the desired locus of points, the equality is true:

The resulting equation defines a parabola with a vertex at a point To reduce the parabola equation to its simplest form, we set and y + 2 = Y then the parabola equation takes the form:

Solution do it with a calculator.
Triangle coordinates are given: A(2,1), B(1,-2), C(-1,0).
1) Vector coordinates
The coordinates of the vectors are found by the formula:
X = x j - x i ; Y = y j - y i

For example, for vector AB

X=1-2=-1; Y=-2-1=-3
AB(-1;-3)
AC(-3;-1)
BC(-2;2)
2) Modules of vectors

3) Angle between straight lines
The angle between the vectors a 1 (X 1; Y 1), a 2 (X 2; Y 2) can be found by the formula:

where a 1 a 2 \u003d X 1 X 2 + Y 1 Y 2
Find the angle between sides AB and AC

γ = arccos(0.6) = 53.13 0
4) Vector projection
Vector projection b per vector a can be found using the formula:

Find the projection of the vector AB onto the vector AC

5) Area of ​​a triangle



Solution


According to the formula we get:

6) Division of the segment in this respect
The radius vector r of the point A, which divides the segment AB in relation to AA:AB = m 1:m 2 , is determined by the formula:

The coordinates of point A are found by the formulas:




Triangle Median Equation
We denote the midpoint of the side BC by the letter M. Then we find the coordinates of the point M by the formulas for dividing the segment in half.


M(0;-1)
We find the equation for the median AM using the formula for the equation of a straight line passing through two given points. The median AM passes through the points A(2;1) and M(0;-1), therefore:

or

or
y=x-1 or y-x+1=0
7) Straight line equation


Equation of line AB

or

or
y = 3x -5 or y -3x +5 = 0
Line AC equation

or

or
y = 1 / 3 x + 1 / 3 or 3y -x - 1 = 0
Line BC equation

or

or
y = -x -1 or y + x +1 = 0
8) The length of the height of the triangle drawn from the vertex A
The distance d from the point M 1 (x 1; y 1) to the straight line Ax + By + C \u003d 0 is equal to the absolute value of the quantity:

Find the distance between point A(2;1) and line BC (y + x +1 = 0)

9) Height equation through vertex C
The line passing through the point M 0 (x 0 ;y 0) and perpendicular to the line Ax + By + C = 0 has a direction vector (A;B) and, therefore, is represented by the equations:


This equation can also be found in another way. To do this, we find the slope k 1 of the straight line AB.
Equation AB: y = 3x -5 i.e. k 1 = 3
Let's find the slope k of the perpendicular from the condition of perpendicularity of two straight lines: k 1 *k = -1.
Substituting instead of k 1 the slope of this straight line, we get:
3k = -1, whence k = -1 / 3
Since the perpendicular passes through the point C(-1,0) and has k = -1 / 3, we will look for its equation in the form: y-y 0 = k(x-x 0).
Substituting x 0 \u003d -1, k \u003d -1 / 3, y 0 \u003d 0 we get:
y-0 = -1 / 3 (x-(-1))
or
y = -1 / 3 x - 1 / 3
Triangle bisector equation
Let us find the bisector of angle A. Denote the point of intersection of the bisector with the side BC by M.
Let's use the formula:

AB equation: y -3x +5 = 0, AC equation: 3y -x - 1 = 0

^A ≈ 53 0
The bisector bisects the angle, hence the angle NAK ≈ 26.5 0
The tangent of slope AB is 3 (because y -3x +5 = 0). The slope angle is 72
^NKA≈ 180 0 - 72 0 = 108 0
^ANK ≈ 180 0 - (108 0 + 26.5 0) ≈ 45.5 0
tg(45.5 0) = 1
The bisector passes through the point A(2,1), using the formula, we have:
y - y 0 \u003d k (x - x 0)
y - 1 = 1(x - 2)
or
y=x-1
Download

Example. The coordinates of the vertices of the triangle ABC are given: A(–3; –1), B(4; 6), C(8; –2).
Required: 1) calculate the length of the side BC; 2) draw up an equation for the side BC; 3) find the interior angle of the triangle at vertex B; 4) make an equation for the height of the AK drawn from the top A; 5) find the coordinates of the center of gravity of a homogeneous triangle (the point of intersection of its medians); 6) make a drawing in the coordinate system.

Exercise. Given the coordinates of the vertices of triangle ABC: A(7;4), B(-9;-8), C(-2;16). Required:

1. write an equation for the median drawn from vertex B and calculate its length.
2. write an equation for the height drawn from vertex A and calculate its length.
3. find the cosine of the interior angle B of triangle ABC.

Example #3. Vertices A(1;1), B(7;4), C(4;5) of a triangle are given. Find: 1) the length of the side AB; 2) internal angle A in radians with an accuracy of 0.001. Make a drawing.
Download

Example #4. Vertices A(1;1), B(7;4), C(4;5) of a triangle are given. Find: 1) the equation of the height drawn through the vertex C ; 2) the equation of the median drawn through the vertex C ; 3) the point of intersection of the heights of the triangle; 4) the length of the height lowered from vertex C. Make a drawing.
Download

Example #5. Vertices of triangle ABC are given: A(-5;0), B(7;-9), C(11;13). Determine: 1) the length of the side AB; 2) equation of sides AB and AC and their slopes; 3) the area of ​​the triangle.

We find the coordinates of the vectors by the formula: X = x j - x i ; Y = y j - y i
here X,Y coordinates of the vector; x i , y i - coordinates of the point A i ; x j , y j - coordinates of point A j
For example, for vector AB
X \u003d x 2 - x 1; Y = y2 - y1
X = 7-(-5) = 12; Y=-9-0=-9
AB(12;-9), AC(16;13), BC(4;22).

Exercise. Given the coordinates of the vertices of the pyramid ABCD. Required:

1. Write the vectors in the ort system and find the modules of these vectors.
2. Find the angle between vectors.
3. Find the projection of a vector onto a vector.
4. Find the area of ​​face ABC.
5. Find the volume of the pyramid ABCD.

Exercise. Find the acute angle between the lines x + y -5 = 0 and x + 4y - 8 = 0 .
Recommendations for a solution. The problem is solved using the Angle between two lines service.
Answer: 30.96o

Example #1. The coordinates of points A1(1;0;2), A2(2;1;1), A3(-1;2;0), A4(-2;-1;-1) are given. Find the length of edge A1A2. Write an equation for the edge A1A4 and the face A1A2A3. Write an equation for the height dropped from point A4 to plane A1A2A3. Find the area of ​​triangle A1A2A3. Find the volume of the triangular pyramid A1A2A3A4.

We find the coordinates of the vectors by the formula: X = x j - x i ; Y = y j - y i ; Z = z j - z i
here X,Y,Z coordinates of the vector; x i , y i , z i - coordinates of the point A i ; x j , y j , z j - coordinates of the point A j ;
So, for the vector A 1 A 2 they will be as follows:
X \u003d x 2 - x 1; Y \u003d y 2 - y 1; Z \u003d z 2 - z 1
X=2-1; Y=1-0; Z=1-2
A 1 A 2 (1;1;-1)
A 1 A 3 (-2;2;-2)
A 1 A 4 (-3;-1;-3)
A 2 A 3 (-3;1;-1)
A 2 A 4 (-4;-2;-2)
A 3 A 4 (-1;-3;-1)
The length of the vector a(X;Y;Z) is expressed in terms of its coordinates by the formula: