How to find extremum points of a function examples. How to find the extremum (minimum and maximum points) of a function. Increasing, decreasing and extrema of a function
Introduction
In many fields of science and in practice, one often encounters the problem of finding the extremum of a function. The fact is that many technical, economic, etc. processes are modeled by a function or several functions that depend on variables - factors that affect the state of the phenomenon being modeled. It is required to find the extrema of such functions in order to determine the optimal (rational) state, process control. So in the economy, the problems of minimizing costs or maximizing profits are often solved - the microeconomic task of the company. In this work, we do not consider modeling issues, but consider only algorithms for finding function extrema in the simplest version, when no restrictions are imposed on the variables (unconditional optimization), and the extremum is sought for only one objective function.
EXTREMA OF THE FUNCTION
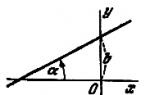
Consider the graph of a continuous function y=f(x) shown in the figure. Function value at point x 1 will be greater than the values of the function at all neighboring points both to the left and to the right of x one . In this case, the function is said to have at the point x 1 max. At the point x The 3 function obviously also has a maximum. If we consider the point x 2 , then the value of the function in it is less than all neighboring values. In this case, the function is said to have at the point x 2 minimum. Similarly for the point x 4 .
Function y=f(x) at the point x 0 has maximum, if the value of the function at this point is greater than its values at all points of some interval containing the point x 0 , i.e. if there is such a neighborhood of the point x 0 , which is for everyone x≠x 0 , belonging to this neighborhood, we have the inequality f(x)<f(x 0 ) .
Function y=f(x) It has minimum at the point x 0 , if there is such a neighborhood of the point x 0 , what is for everyone x≠x 0 belonging to this neighborhood, we have the inequality f(x)>f(x0.
The points at which the function reaches its maximum and minimum are called extremum points, and the values of the function at these points are the extrema of the function.
Let us pay attention to the fact that a function defined on a segment can reach its maximum and minimum only at points contained within the segment under consideration.
Note that if a function has a maximum at a point, this does not mean that at this point the function has the maximum value in the entire domain. In the figure discussed above, the function at the point x 1 has a maximum, although there are points at which the values of the function are greater than at the point x 1 . In particular, f(x 1) < f(x 4) i.e. the minimum of the function is greater than the maximum. From the definition of the maximum, it only follows that this is the largest value of the function at points sufficiently close to the maximum point.
Theorem 1. (A necessary condition for the existence of an extremum.) If a differentiable function y=f(x) has at the point x=x 0 extremum, then its derivative at this point vanishes.
Proof. Let, for definiteness, at the point x 0 the function has a maximum. Then for sufficiently small increments Δ x we have f(x 0 + Δ x)
Passing in these inequalities to the limit as Δ x→ 0 and taking into account that the derivative f "(x 0) exists, and hence the limit on the left does not depend on how Δ x→ 0, we get: for Δ x → 0 – 0 f"(x 0) ≥ 0 and at Δ x → 0 + 0 f"(x 0) ≤ 0. Since f"(x 0) defines a number, then these two inequalities are compatible only if f"(x 0) = 0.
The proved theorem states that the maximum and minimum points can only be among those values of the argument for which the derivative vanishes.
We have considered the case when a function has a derivative at all points of a certain segment. What happens when the derivative does not exist? Consider examples.
y=|x|.
The function does not have a derivative at a point x=0 (at this point, the graph of the function does not have a definite tangent), but at this point the function has a minimum, since y(0)=0, and for all x≠ 0y > 0.
has no derivative at x=0, since it goes to infinity when x=0. But at this point, the function has a maximum. has no derivative at x=0, because at x→0. At this point, the function has neither a maximum nor a minimum. Really, f(x)=0 and at x<0f(x)<0, а при x>0f(x)>0.Thus, from the given examples and the formulated theorem it is clear that the function can have an extremum only in two cases: 1) at the points where the derivative exists and is equal to zero; 2) at the point where the derivative does not exist.
However, if at some point x 0 we know that f"(x 0 ) =0, then it cannot be concluded from this that at the point x 0 the function has an extremum.
For example.
.But point x=0 is not an extremum point, since to the left of this point the function values are located below the axis Ox, and above on the right.
Values of an argument from the domain of a function, for which the derivative of the function vanishes or does not exist, are called critical points.
It follows from the foregoing that the extremum points of a function are among the critical points, and, however, not every critical point is an extremum point. Therefore, to find the extremum of the function, you need to find all the critical points of the function, and then examine each of these points separately for maximum and minimum. For this, the following theorem serves.
Theorem 2. (A sufficient condition for the existence of an extremum.) Let the function be continuous on some interval containing the critical point x 0 , and is differentiable at all points of this interval (except, perhaps, the point itself x 0). If, when passing from left to right through this point, the derivative changes sign from plus to minus, then at the point x = x 0 the function has a maximum. If, when passing through x 0 from left to right, the derivative changes sign from minus to plus, then the function has a minimum at this point.
Thus, if
f"(x)>0 at x<x 0 and f"(x)< 0 at x > x 0 , then x 0 - maximum point;
at x<x 0 and f "(x)> 0 at x > x 0 , then x 0 is the minimum point.Proof. Let us first assume that when passing through x 0, the derivative changes sign from plus to minus, i.e. for all x close to the point x 0 f "(x)> 0 for x< x 0 , f"(x)< 0 for x > x 0 . Let us apply the Lagrange theorem to the difference f(x) - f(x 0 ) = f "(c)(x- x 0), where c lies between x and x 0 .
Let x< x 0 . Then c< x 0 and f "(c)> 0. That's why f "(c)(x-x 0)< 0 and, therefore,
f(x) - f(x 0 )< 0, i.e. f(x)< f(x 0 ).
Let x > x 0 . Then c>x 0 and f"(c)< 0. Means f "(c)(x-x 0)< 0. That's why f(x) - f(x 0 ) <0,т.е.f(x)< f(x 0 ) .
Thus, for all values x close enough to x 0 f(x)< f(x 0 ) . And this means that at the point x 0 the function has a maximum.
The second part of the minimum theorem is proved similarly.
Let us illustrate the meaning of this theorem in the figure. Let f"(x 1 ) =0 and for any x, close enough to x 1 , the inequalities
f"(x)< 0 at x< x 1 , f "(x)> 0 at x > x 1 .
Then to the left of the point x 1 the function is increasing, and decreasing on the right, therefore, when x = x 1 function goes from increasing to decreasing, that is, it has a maximum.
Similarly, one can consider the points x 2 and x 3 .
Schematically, all of the above can be depicted in the picture:
The rule for studying the function y=f(x) for an extremum
Find the scope of a function f(x).
Find the first derivative of a function f"(x).
Determine critical points, for this:
find the real roots of the equation f"(x)=0;
find all values x under which the derivative f"(x) does not exist.
Determine the sign of the derivative to the left and right of the critical point. Since the sign of the derivative remains constant between two critical points, it suffices to determine the sign of the derivative at any one point to the left and at one point to the right of the critical point.
Calculate the value of the function at the extremum points.
As you can see, this sign of the extremum of the function requires the existence of a derivative at least up to the second order at the point .
Example.
Find the extrema of the function .
Solution.
Let's start with the scope: 
Let's differentiate the original function: 
x=1, that is, it is the point of a possible extremum. We find the second derivative of the function and calculate its value at x=1:

Therefore, by the second sufficient extremum condition, x=1- maximum point. Then  is the maximum of the function.
is the maximum of the function.
Graphic illustration.

Answer:
![]()
The third sufficient condition for the extremum of a function.
Let the function y=f(x) has derivatives up to n-th order in -neighbourhood of a point and derivatives up to n+1 th order at the point itself. Let and .
Example.
Find extremum points of a function ![]() .
.
Solution.
The original function is an entire rational one, its domain of definition is the entire set of real numbers.
Let's differentiate the function: 
The derivative vanishes when ![]() , therefore, these are the points of a possible extremum. Let us use the third sufficient condition for an extremum.
, therefore, these are the points of a possible extremum. Let us use the third sufficient condition for an extremum.
We find the second derivative and calculate its value at the points of a possible extremum (we will omit intermediate calculations): 
Therefore, is the maximum point (for the third sufficient sign of the extremum, we have n=1 and ).
To clarify the nature of the points ![]() find the third derivative and calculate its value at these points:
find the third derivative and calculate its value at these points: 
Therefore, is the inflection point of the function ( n=2 and ).
It remains to deal with the point. We find the fourth derivative and calculate its value at this point: 
Therefore, is the minimum point of the function.
Graphic illustration.

Answer:
The maximum point is the minimum point of the function.
10. Extremums of a function Definition of an extremum
The function y = f(x) is called increasing (waning) in some interval if for x 1< x 2 выполняется неравенство (f(x 1) < f (x 2) (f(x 1) >f(x2)).
If a differentiable function y = f(x) on a segment increases (decreases), then its derivative on this segment f "(x) 0
(f "(x) 0).
Dot x about called local maximum point (minimum) of the function f(x) if there is a neighborhood of the point x about, for all points of which the inequality f(x) ≤ f(x o) (f(x) ≥ f(x o)) is true.
The maximum and minimum points are called extremum points, and the values of the function at these points are its extrema.
extremum points
Necessary conditions for an extremum. If point x about is an extremum point of the function f (x), then either f "(x o) \u003d 0, or f (x o) does not exist. Such points are called critical, where the function itself is defined at the critical point. The extrema of a function should be sought among its critical points.
The first sufficient condition. Let x about- critical point. If f "(x) when passing through a point x about changes the plus sign to minus, then at the point x about the function has a maximum, otherwise it has a minimum. If the derivative does not change sign when passing through a critical point, then at the point x about there is no extremum.
The second sufficient condition. Let the function f(x) have a derivative f "(x) in a neighborhood of the point x about and the second derivative at the very point x about. If f "(x o) \u003d 0,\u003e 0 (<0), то точка x about is a local minimum (maximum) point of the function f(x). If =0, then one must either use the first sufficient condition or involve higher derivatives.
On a segment, the function y = f(x) can reach its minimum or maximum value either at critical points or at the ends of the segment.
Example 3.22. Find the extrema of the function f(x) = 2x 3 - 15x 2 + 36x - 14.
Solution. Since f "(x) \u003d 6x 2 - 30x +36 \u003d 6 (x - 2) (x - 3), then the critical points of the function x 1 \u003d 2 and x 2 \u003d 3. Extreme points can only be at these points. So as when passing through the point x 1 \u003d 2, the derivative changes sign plus to minus, then at this point the function has a maximum.When passing through the point x 2 \u003d 3, the derivative changes sign minus to plus, therefore, at the point x 2 \u003d 3, the function has a minimum. Having calculated the values of the function at the points x 1 = 2 and x 2 = 3, we find the extrema of the function: maximum f (2) = 14 and minimum f (3) = 13.
A simple algorithm for finding extrema..
- Finding the derivative of a function
- Equate this derivative to zero
- We find the values of the variable of the resulting expression (the values of the variable at which the derivative is converted to zero)
- We divide the coordinate line into intervals with these values (at the same time, we should not forget about the break points, which also need to be applied to the line), all these points are called “suspicious” points for the extremum
- We calculate on which of these intervals the derivative will be positive, and on which it will be negative. To do this, you need to substitute the value from the interval into the derivative.
Of the points suspected of an extremum, it is necessary to find exactly . To do this, we look at our gaps on the coordinate line. If, when passing through some point, the sign of the derivative changes from plus to minus, then this point will be maximum, and if from minus to plus, then minimum.
To find the largest and smallest value of a function, you need to calculate the value of the function at the ends of the segment and at the extremum points. Then choose the largest and smallest value.
Consider an example
We find the derivative and equate it to zero:
We apply the obtained values of the variables to the coordinate line and calculate the sign of the derivative on each of the intervals. Well, for example, for the first take-2
, then the derivative will be-0,24
, for the second take0
, then the derivative will be2
, and for the third we take2
, then the derivative will be-0.24. We put down the appropriate signs.
We see that when passing through point -1, the derivative changes sign from minus to plus, that is, it will be a minimum point, and when passing through 1, from plus to minus, respectively, this is a maximum point.
Let us turn to the graph of the function y \u003d x 3 - 3x 2. Consider the neighborhood of the point x = 0, i.e. some interval containing this point. It is logical that there is such a neighborhood of the point x \u003d 0 that the function y \u003d x 3 - 3x 2 takes the largest value in this neighborhood at the point x \u003d 0. For example, on the interval (-1; 1) the largest value equal to 0, the function takes at the point x = 0. The point x = 0 is called the maximum point of this function.
Similarly, the point x \u003d 2 is called the minimum point of the function x 3 - 3x 2, since at this point the value of the function is not greater than its value at another point in the vicinity of the point x \u003d 2, for example, the neighborhood (1.5; 2.5).
Thus, the point x 0 is called the maximum point of the function f (x) if there is a neighborhood of the point x 0 - such that the inequality f (x) ≤ f (x 0) is satisfied for all x from this neighborhood.
For example, the point x 0 \u003d 0 is the maximum point of the function f (x) \u003d 1 - x 2, since f (0) \u003d 1 and the inequality f (x) ≤ 1 is true for all values of x.
The minimum point of the function f (x) is called the point x 0 if there is such a neighborhood of the point x 0 that the inequality f (x) ≥ f (x 0) is satisfied for all x from this neighborhood.
For example, the point x 0 \u003d 2 is the minimum point of the function f (x) \u003d 3 + (x - 2) 2, since f (2) \u003d 3 and f (x) ≥ 3 for all x.
Extreme points are called minimum points and maximum points.
Let us turn to the function f(x), which is defined in some neighborhood of the point x 0 and has a derivative at this point.
If x 0 is an extremum point of a differentiable function f (x), then f "(x 0) \u003d 0. This statement is called Fermat's theorem.
Fermat's theorem has a clear geometric meaning: at the extremum point, the tangent is parallel to the x-axis and therefore its slope
f "(x 0) is zero.
For example, the function f (x) \u003d 1 - 3x 2 has a maximum at the point x 0 \u003d 0, its derivative f "(x) \u003d -2x, f "(0) \u003d 0.
The function f (x) \u003d (x - 2) 2 + 3 has a minimum at the point x 0 \u003d 2, f "(x) \u003d 2 (x - 2), f "(2) \u003d 0.
Note that if f "(x 0) \u003d 0, then this is not enough to assert that x 0 is necessarily the extremum point of the function f (x).
For example, if f (x) \u003d x 3, then f "(0) \u003d 0. However, the point x \u003d 0 is not an extremum point, since the function x 3 increases on the entire real axis.
So, the extremum points of a differentiable function must be sought only among the roots of the equation
f "(x) \u003d 0, but the root of this equation is not always an extremum point.
Stationary points are points at which the derivative of a function is equal to zero.
Thus, in order for the point x 0 to be an extremum point, it is necessary that it be a stationary point.
Consider sufficient conditions for a stationary point to be an extremum point, i.e. conditions under which a stationary point is a minimum or maximum point of a function.
If the derivative to the left of the stationary point is positive, and to the right it is negative, i.e. derivative changes sign "+" to sign "-" when passing through this point, then this stationary point is the maximum point.
Indeed, in this case, to the left of the stationary point, the function increases, and to the right, it decreases, i.e. this point is the maximum point.
If the derivative changes sign "-" to sign "+" when passing through a stationary point, then this stationary point is a minimum point.
If the derivative does not change sign when passing through a stationary point, i.e. the derivative is positive or negative to the left and to the right of the stationary point, then this point is not an extremum point.
Let's consider one of the problems. Find the extremum points of the function f (x) \u003d x 4 - 4x 3.
Solution.
1) Find the derivative: f "(x) \u003d 4x 3 - 12x 2 \u003d 4x 2 (x - 3).
2) Find stationary points: 4x 2 (x - 3) \u003d 0, x 1 \u003d 0, x 2 \u003d 3.
3) Using the interval method, we establish that the derivative f "(x) \u003d 4x 2 (x - 3) is positive for x\u003e 3, negative for x< 0 и при 0 < х < 3.
4) Since when passing through the point x 1 \u003d 0, the sign of the derivative does not change, this point is not an extremum point.
5) The derivative changes the sign "-" to the sign "+" when passing through the point x 2 \u003d 3. Therefore, x 2 \u003d 3 is the minimum point.
site, with full or partial copying of the material, a link to the source is required.
From this article, the reader will learn about what an extremum of functional value is, as well as about the features of its use in practice. The study of such a concept is extremely important for understanding the foundations of higher mathematics. This topic is fundamental to a deeper study of the course.
In contact with
What is an extreme?
In the school course, many definitions of the concept of "extremum" are given. This article is intended to give the deepest and clearest understanding of the term for those who are ignorant of the issue. So, the term is understood to what extent the functional interval acquires a minimum or maximum value on a particular set.
The extremum is both the minimum value of the function and the maximum at the same time. There is a minimum point and a maximum point, that is, the extreme values of the argument on the graph. The main sciences in which this concept is used:
- statistics;
- machine control;
- econometrics.
Extreme points play an important role in determining the sequence of a given function. The coordinate system on the graph at its best shows the change in extreme position depending on the change in functionality.
Extrema of the derivative function
There is also such a thing as a "derivative". It is necessary to determine the extremum point. It is important not to confuse the minimum or maximum points with the largest and smallest values. These are different concepts, although they may seem similar.
The value of the function is the main factor in determining how to find the maximum point. The derivative is not formed from the values, but exclusively from its extreme position in one order or another.
The derivative itself is determined based on the data of the extreme points, and not the largest or smallest value. In Russian schools, the line between these two concepts is not clearly drawn, which affects the understanding of this topic in general.
Let's now consider such a thing as a "sharp extremum". To date, there is an acute minimum value and an acute maximum value. The definition is given in accordance with the Russian classification of critical points of a function. The concept of an extremum point is the basis for finding critical points on a chart.

To define such a concept, Fermat's theorem is used. It is the most important in the study of extreme points and gives a clear idea of their existence in one form or another. To ensure extremeness, it is important to create certain conditions for decreasing or increasing on the chart.
To accurately answer the question "how to find the maximum point", you must follow these provisions:
- Finding the exact area of definition on the chart.
- Search for the derivative of a function and an extremum point.
- Solve standard inequalities for the domain of the argument.
- Be able to prove in which functions a point on a graph is defined and continuous.

Attention! The search for a critical point of a function is possible only if there is a derivative of at least the second order, which is ensured by a high proportion of the presence of an extremum point.
Necessary condition for the extremum of the function
In order for an extremum to exist, it is important that there are both minimum points and maximum points. If this rule is observed only partially, then the condition for the existence of an extremum is violated.

Each function in any position must be differentiated in order to identify its new meanings. It is important to understand that the case when a point vanishes is not the main principle of finding a differentiable point.
A sharp extremum, as well as a function minimum, is an extremely important aspect of solving a mathematical problem using extreme values. In order to better understand this component, it is important to refer to the tabular values for the assignment of the functional.
| A complete exploration of meaning | Plotting a Value |
| 1. Determination of points of increase and decrease of values. 2. Finding break points, extremum and intersection with coordinate axes. 3. The process of determining changes in position on the chart. 4. Determination of the index and direction of convexity and convexity, taking into account the presence of asymptotes. 5. Creation of a summary table of the study in terms of determining its coordinates. 6. Finding intervals of increase and decrease of extreme and acute points. 7. Determination of the convexity and concavity of the curve. 8. Building a graph based on the study allows you to find a minimum or maximum. |
The main element, when it is necessary to work with extremums, is the exact construction of its graph. School teachers do not often pay maximum attention to such an important aspect, which is a gross violation of the educational process. The graph is built only on the basis of the results of the study of functional data, the definition of sharp extrema, as well as points on the graph. Sharp extrema of the derivative of a function are displayed on a plot of exact values using the standard procedure for determining asymptotes. The maximum and minimum points of the function are accompanied by more complex plotting. This is due to a deeper need to work out the problem of a sharp extremum. It is also necessary to find the derivative of a complex and simple function, since this is one of the most important concepts in the problem of extremum. |
Functional extremum
In order to find the above value, you must adhere to the following rules:
- determine the necessary condition for the extremal ratio;
- take into account the sufficient condition of the extreme points on the graph;
- carry out the calculation of an acute extremum.
There are also concepts such as weak minimum and strong minimum. This must be taken into account when determining the extremum and its exact calculation. At the same time, sharp functionality is the search and creation of all the necessary conditions for working with the function graph.